Comentarios
← vista completaPublicado el 8 de abril de 2020 | http://doi.org/10.5867/medwave.2020.03.7874
Fortalezas y limitaciones de los modelos matemáticos en las pandemias: el caso de COVID-19 en Chile
Strengths and limitations of mathematical models in pandemics—the case of COVID-19 in Chile
Resumen
Este breve documento se centra en el papel de los modelos matemáticos para analizar el impacto de las pandemias en los recursos de salud y las diferentes trade-off que pueden estar presente. Existe una gran cantidad de literatura que sugiere que los modelos matemáticos pueden ser útiles para estimar cuánto equipo e infraestructura adicionales pueden ser necesarios para mitigar un aumento en la demanda de servicios de salud durante un brote a gran escala de una enfermedad infecciosa. Comento sobre el papel crucial de estos modelos con un enfoque especial en sus fortalezas y limitaciones.
Introducción
Este documento está motivado por la pandemia actual de coronavirus (COVID-19) en todo el mundo y particularmente en Chile. Un artículo reciente de Gutiérrez-Aguilar et al. (2020)[1] aborda este problema crucial de disponibilidad de recursos de salud para hacer frente al brote de este nuevo coronavirus. Este coronavirus está relacionado con el SARS-CoV teniendo tiempos de incubación y generación similares, pero con una tasa más baja de progresión a una enfermedad grave y muerte si se tiene acceso a un adecuado apoyo médico.[2] Sin embargo, la transmisión de COVID-19 de persona a persona ha demostrado ser altamente eficiente y ahora está presente en más de 200 países y territorios.[3],[4] La enfermedad causada por este virus tiende a ser más grave en los adultos mayores y los enfermos crónicos. Una fracción de las personas infectadas puede que tenga que ser admitido a una unidad de cuidados intensivos (UCI) y requerir ventilación mecánica. Este es el principal problema que afecta tanto a los países avanzados como a los países en vías de desarrollo.[5] La razón es sencilla de entender. Las camas de la UCI y los ventiladores mecánicos son recursos limitados, y su número en un país determinado es un equilibrio suficiente para la demanda habitual de atención médica. Podemos decir que la mayoría de las veces, la limitación de los recursos de la UCI no es vinculante en sentido estricto. Sin embargo, para el estallido de COVID-19, esto ya no es cierto, y países como Italia han fracasado en proveer este equipamiento de cuidados intensivos, con la consecuencia de aumentar su tasa de mortalidad.[6] Todo esto hace que sea esencial contar con modelos matemáticos para pronosticar correctamente la demanda de recursos de la UCI. En este artículo, analizo los elementos a considerar para realizar esta tarea con éxito.
Modelos pequeños versus grandes
Los modelos matemáticos pueden usarse para estimar diferentes tipos de variables y diferir en su metodología. La variable o el modelo que se use dependerá de la pregunta a responder. Por ejemplo, podríamos usar un modelo para estimar el número de personas infectadas en base a una suposición sobre el número básico de reproducción (R0) o podríamos usar datos sobre personas infectadas para estimar R0. Si la enfermedad tiene un comportamiento conocido, entonces se puede suponer que algunos parámetros son conocidos u observados. Sin embargo, si la enfermedad es nueva – como es el caso del COVID-19 – entonces tenemos que hacer frente a todos los problemas asociados con la estimación de dichos parámetros. Un valor de parámetro que es crítico conocer es R0 y este puede estar definido por una función de variables con diferentes valores de parámetros asociados. Por lo tanto, dependiendo de la concepción teórica referencial, el R0 va a ser diferente según los supuestos que se hagan. En términos matemáticos,
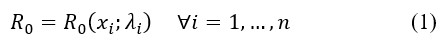
La ecuación (1) muestra que el número de reproducción básico depende de un conjunto de variables y hay un parámetro λi relacionado con cada variable xi. Por lo tanto, si queremos estimar R0, entonces necesitamos saber qué variables deben incluirse. Asumiendo que conocemos la especificación correcta del modelo, entonces necesitamos estimar los parámetros λi. En esta etapa, podríamos encontrar dos problemas principales: (i) errores de medición en los datos y (ii) autoselección de individuos que componen dicha base. Ambos problemas pueden abordarse en términos estadísticos, pero es necesario reunir nueva información para hacer las correcciones o ajustes necesarios. Todo esto es analizado en una configuración estática. Es decir, el tiempo no está jugando un papel hasta ahora. Sin embargo, como las variables, xi, evolucionan con el tiempo, t, entonces R0 también cambiará. Esto se puede representar como,
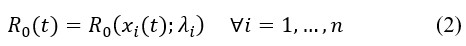
La ecuación (2) implica que el número de reproducción básico puede evolucionar con el tiempo a medida que las variables lo hacen, incluso si suponemos homogeneidad en el tiempo para los coeficientes paramétricos λi. Por lo tanto, el ejercicio de estimación de R0 no es trivial.
La estimación de cualquier parámetro a emplear en un modelo matemático está usualmente acosada con el mismo nivel de complejidad. Qué tan simple o complejo son estas estimaciones dependerá de la disponibilidad de datos y/o del conocimiento sobre el fenómeno en estudio.
La discusión previa está dirigida a resaltar la importancia de comprender la naturaleza de los parámetros que entran en un modelo que se usa para predecir o pronosticar una variable dada o un conjunto de ellas. Los parámetros que deben conocerse dependen de los supuestos subyacentes del modelo. Por lo general, a medida que aumenta el nivel de complejidad, también lo hace el número de parámetros a conocer. La mayor complejidad en el modelo a menudo se asocia con algunas ganancias en la representación de la realidad a costa de necesitar más información (conocer más parámetros)[7]. Si el modelo debe ser grande o pequeño depende de la situación y/o pregunta a responder. Debemos tener en cuenta que el uso de un modelo grande con valores de parámetros poco precisos podría causar más daño que bien, lo que me lleva a la siguiente sección.
Todos los modelos están equivocados, pero algunos son útiles.
El título de esta sección se atribuye al estadístico George Box, quien expresó la idea de que un modelo, incluso complejo, es una simplificación de la realidad. No obstante, algunos modelos pueden ser muy útiles en la comprensión de un fenómeno, o para pronosticar una variable. Los economistas han tenido que abordar el problema de la construcción de modelos útiles y aplicables durante más de un siglo. En Turnovsky (2011)[8] encontramos un consejo proporcionado por el premio Nobel Robert Solow sobre cómo elaborar modelos útiles y exitosos. Esto se puede resumir en las siguientes tres ideas:
- Hazlo simple.
- Hazlo bien.
- Hazlo plausible.
Subyacente a esta sugerencia es la idea de que los modelos deben tener el nivel de complejidad justo, lo que significa que los modelos no deben ser más simple que lo que sea necesario, pero tampoco no más complejo de lo necesario. Lograr este equilibrio es, por supuesto, es altamente sofisticado. Sin embargo, un análisis riguroso del problema que se está abordando debería proveer luces sobre los supuestos que se deben hacer y los valores de los parámetros que están disponibles. El artículo de Córdova-Lepe et al. (2020) es un buen ejemplo de esto. Construyen un modelo que hace varias suposiciones que son plausibles y usan un modelo que es lo suficientemente simple como para ser manejable, y lo suficientemente elaborado como para proporcionar información útil. Ese es el nivel justo de complejidad.
COVID-19 y el colapso del sistema hospitalario
Continuando con la discusión de Córdova-Lepe et al. (2020), estudian el esfuerzo mínimo diario para que el sistema de salud no colapse durante el brote de COVID-19. En su modelo, los supuestos se indican claramente, así como el análisis de sensibilidad que realizaron para estimar el impacto global de los diferentes parámetros. Reconocen que un parámetro que debe ser estimado y que desconocen es el esfuerzo diario para reducir el contagio. Sin embargo, demuestran con la ayuda de simulaciones numéricas que si existen pequeños cambios en el valor de dicho parámetro, los efectos sobre la evolución de las necesidades hospitalarias es muy significativo. Esto es que dependiendo de su valor podría determinar el colapso o no del sistema hospitalario. Establecer fechas para el colapso del sistema de salud sin observar valores de parámetros precisos para el fenómeno COVID-19 es casi imposible en esta etapa, incluso con un modelo simple que requiere poca información. Los modelos pequeños como este pueden ser extremadamente útiles para resaltar que algunas acciones son cruciales y, al mismo tiempo, que las pequeñas diferencias pueden, en efecto, marcar una gran diferencia. Específicamente, encuentran que, para frenar la epidemia de esta enfermedad respiratoria, acciones como el aislamiento y el distanciamiento social podrían significar la diferencia entre el colapso del sistema de salud en distintos tiempos o evitar su colapso.[9] También señalan que estas medidas pueden tener impactos económicos indeseables, lo cual no está modelado en su documento porque no es su enfoque. No hace falta decir que la economía es un aspecto relevante para los tomadores de decisiones.[10]
Conclusiones finales
La comprensión de las limitaciones de los modelos es fundamental para proporcionar información útil para policymakers y público en general. Al estudiar modelos matemáticos, se debe poner más esfuerzo en comprender el impacto de los supuestos subyacentes en los resultados o predicciones. Del mismo modo, se debe realizar un esfuerzo más considerable para analizar la sensibilidad del modelo a diferentes valores paramétricos. Además, los rangos numéricos elegidos deben justificarse de forma transparente proporcionando todas las fuentes disponibles. Los criterios anteriores son normas recomendadas para mejorar la credibilidad de nuestros análisis por parte de otros modeladores, los planificadores y los tomadores de decisiones. Una vez que un brote a gran escala de una enfermedad infecciosa ocurre, usualmente no hay mucho tiempo para construir modelos o estimar parámetros. Por lo tanto, tener planes de contingencia basados en diferentes escenarios y modelos de predicción es vital para superar una crisis de salud exitosamente.

