Análisis
← vista completaPublicado el 27 de marzo de 2020 | http://doi.org/10.5867/medwave.2020.02.7861
Número de casos COVID-19 en Chile a 120 días con datos al 21/03/2020 y umbral del esfuerzo diario para aplanar la epi-curva
Number of COVID-19 cases in Chile at 120 days with data at 21/03/2020 and threshold of daily effort to flatten the epi-curve
Resumen
Realizamos una prospectiva básica, con datos al 21/03/2020 de la evolución del número de casos COVID-19 diarios en Chile con datos del Ministerio de Salud. Asumiendo un crecimiento aritmético en la segunda variación de los datos, se presenta un modelo de ajuste cúbico que estima en más de 100 mil casos a 120 días y que es consistente con los datos registrados a la fecha. Además, se interviene un modelo de casos totales exponencial, para representar en él (mediante un parámetro) el esfuerzo diario por rebajar una elevada primera tasa de crecimiento diario. Este modelo se simula con distinto escenarios numéricos de factibilidad y prevalencia futura deseada.
Ideas clave
- Ante el aumento de los casos de COVID-19 en Chile se requiere conocer si los casos totales llegarán a colapsar la capacidad hospitalaria.
- Mediante un modelo simplificado se realiza una proyección a 120 días.
- Además, se analiza el efecto controlador que tiene la existencia de un parámetro relacionado con el esfuerzo por disminuir la tasa porcentual diaria de propagación.
- La premura y una matemática accesible y que cubra el pequeño rango de datos, implica como limitante trabajar los parámetros como valor determinado y no como distribución.
Introducción
Ante el surgimiento de un nuevo coronavirus (o de cualquier epidemia) es muy importante efectuar estimaciones a futuro; no hay país que quiera tener 627 muertes un día y al siguiente (21/03/2020) otras 793, como en Italia[1]. Para no llegar en la misma fecha a cifras de 25 mil contagiados con aproximadamente 1620 en unidades de cuidado intensivo, como en España[2], se requiere la construcción de proyecciones estructuralmente confiables y a la vez consistentes con el historial epidemiológico que permitan apreciar tanto la acción como la inacción frente al problema. El tener modelos matemáticos-estadísticos de predicción, por ejemplo, de los casos que periódicamente se incorporan es un soporte a la experiencia de los especialistas para la apreciación de si las medidas de control se están reflejando en la reducción de las cifras. En el cambio de estrategia del Reino Unido frente a COVID-19, influyó el pronóstico de un modelo matemático[3]: habría un total de 510 mil muertes y un contexto de 80% de la población contagiada si no se implementaban medidas de supresión.
La anticipación y el uso de la experiencia propia y la de otros países o regiones afectadas parecen ser el camino. Esta construcción de perspectiva del problema en términos numéricos también es necesaria para fortalecer la responsabilidad social que debemos tener los individuos sobre la magnitud del problema y su relación con nuestra conducta; ayuda a generar mejores condiciones de recepción de las medidas de control (por lo general basadas en una serie de restricciones) que la autoridad sugiera, ordene e implemente.
El Ministerio de Salud de Chile adelantó que, en cuanto al número de camas hospitalarias, estaría preparado para soportar a 250 mil casos[4]. ¿Será suficiente? Esta pregunta es clave, más aún cuando la canciller Ángela Merkel afirmó que sobre el 70% de la población alemana puede contagiarse[5]. Respecto a la expansión de Covid-19, a la fecha Chile ha entrado en la fase 4 (positivos sin trazabilidad y en algunos territorios con circulación comunitaria). Hacia el día 12/03/2020, un medio de prensa comunicó una proyección de los datos para junio del presente de 30 mil contagiados totales[6]. Ese mismo día, los autores del presente artículo comunicaron, en un diario de circulación nacional, una estimación a 120 días de un total de 100 mil casos[7].
En la primera etapa de propagación de una enfermedad contagiosa, más precisamente cuando todavía un porcentaje muy pequeño de la población se encuentra en proceso infeccioso, un parámetro clave es la tasa porcentual de crecimiento diario. Si este parámetro se mantiene en el tiempo, el crecimiento de los casos totales se puede modelar siguiendo una formulación de interés compuesto, siguiendo dicha tasa, un crecimiento geométrico. Respecto a COVID-19 existen regiones del globo que exhiben secuencias de total de casos que han exhibido una tasa diaria del 20%, como España[8]. Otro ejemplo es el de Italia que, hacia el 26/02/2020, presentaba según informaciones de prensa un crecimiento diario de 25%[9]. En Chile, a menos de dos semanas de la llegada, dicha tasa diaria era superior al 30%. Es claro que proyectar los casos a futuro manteniendo esta tasa no es sostenible—a poco andar las cifras son del orden de millones—por lo que en el presente artículo trabajamos un modelo que permite calcular o estimar el valor del esfuerzo diario (medido en porcentaje de reducción de la tasa de contagio inicial) a realizar que permita (con suficiencia) alcanzar las metas de prevalencia que algún controlador se fije. El cómo medir este parámetro de esfuerzo, definido por múltiples inputs, es una pregunta abierta y requiere de mucha mayor investigación. Nuestro objetivo es establecer por escrito los elementos estadísticos y matemáticos que sustentaron la primigenia proyección de 100 mil casos, como también, detallar algunos alcances y limitaciones.
Observaciones metodológicas
El modelamiento matemático en epidemiología juega el rol de la cartografía en la navegación, una representación que dibuja el paisaje y orienta el proceder. Los nombres de Daniel Bernoulli (inoculación contra la viruela, 1766)[10], Ronald Ross (comportamiento epidémico, 1910)[11] y de Kermack-McKendrick (comportamiento de los brotes, 1927)[12] con sus útiles modelos, desde lo teórico y también lo práctico, de algún modo inauguraron la epidemiología matemática (soporte del análisis epidemiológico), marcando un lento principio que hoy está en la fase exponencial de desarrollo exhibiendo una sorprendente y bien documentada capacidad predictiva.
Hay dos tipos de modelos predictivos de orden cuantitativo: los extremos y sus híbridos. Están por un lado los modelos con base en las herramientas que tiene la estadística (a posteriori) y por otro los modelos matemáticos (a priori) en stricto sensu. Los primeros se enfocan en datos y otra información de interés, por ejemplo, la experiencia de expertos. En cuanto a los segundos, estos apuntan a conocer las consecuencias lógicas (las que pueden ser relacionales o numéricas) de conjeturas acerca de relaciones entre las variables descriptivas que permiten (es lo esperado) explicar a grandes rasgos los determinantes teóricos de la dinámica del proceso.
Un modelo matemático o estadístico para la comprensión y proyección de COVID-19 será siempre una maqueta conceptual para representar algún aspecto de la realidad. No todo puede estar representado, por lo que siempre se ha de construir conociendo el alcance que se precise o conforme al mandante. Resultan determinantes definir qué interrogantes debiera ayudar a responder el modelo (valor de uso), cuál es la precisión deseada de las respuestas (grado de confianza), cuál es la disponibilidad de recurso humano (científico y técnico) al momento de querer modelar. Por otro lado, entre tener un gran y complejo modelo que intente responderlo todo o varios que apunten a inquietudes específicas y proyecciones locales, podría resultar más acertado, plausible y económico lo último. En nuestro caso, la intención es optar por la simplicidad matemática en cuanto al número de variables, parámetros y tipos de cálculo, con el fin de facilitar la comprensión a un amplio espectro de lectores y comunicadores sociales sin pérdida de rigor y en forma oportuna.
En la sección “Modelo de progresión geométrica” observaremos que la opción de un modelo matemático de tipo exponencial a tasa constante (o de progresión geométrica) no es sostenible a muy largo plazo, pues por las tasas actuales determinan un crecimiento demasiado rápido y de alta sensibilidad a leves variaciones en la tasa como se verá. El modelo de la sección “Proyección cúbica” en principio no intenta explicar el fenómeno y corresponde a un ajuste cúbico. En ese sentido, es un modelo puramente estadístico donde los datos determinan. Sin embargo, exceptuando los primeros días en que priman los casos importados, después tiene buena coincidencia con los datos. Además, el estudio de sus variaciones sugiere, como simple interpretación, la acción de un esfuerzo por llevar la tasa a la baja. Esta idea es lo que recoge la sección “Proyecciones exponenciales con control” en que volvemos a postular un modelo ahora matemático que explique y proyecte la acción de un esfuerzo sostenido (día a día) por bajar la tasa de contagio.
La población objetivo es la de todo el país y la variable principal a considerar es el número total de casos confirmados en Chile COVID-19 diarios, según comunicados por el Ministerio de Salud. La curva de incidencia, con o sin oponer mitigación, siempre es acampanada. Notemos que de no oponer medidas esta curva lentifica, con un R0~3[13],[14] para (COVID-19) y una población de 18 millones, cuando restan entre 1, 2 y 6 millones de susceptibles de infectar. Al no desear ese orden de cifras, asumiremos que nos mantenemos en la etapa convexa inicial de la curva. Como solo perseguimos un orden de magnitud de la proyección (miles, decenas o centenas de miles), no hacemos el análisis de rango de confianza del ajuste. Optamos, más bien, por objetos matemáticos de la cultura general, como mezclas de progresiones de aritméticas y geométricas. Además, hacemos representaciones vía tablas de datos numéricos y gráficas estándar.
Modelo de progresión geométrica
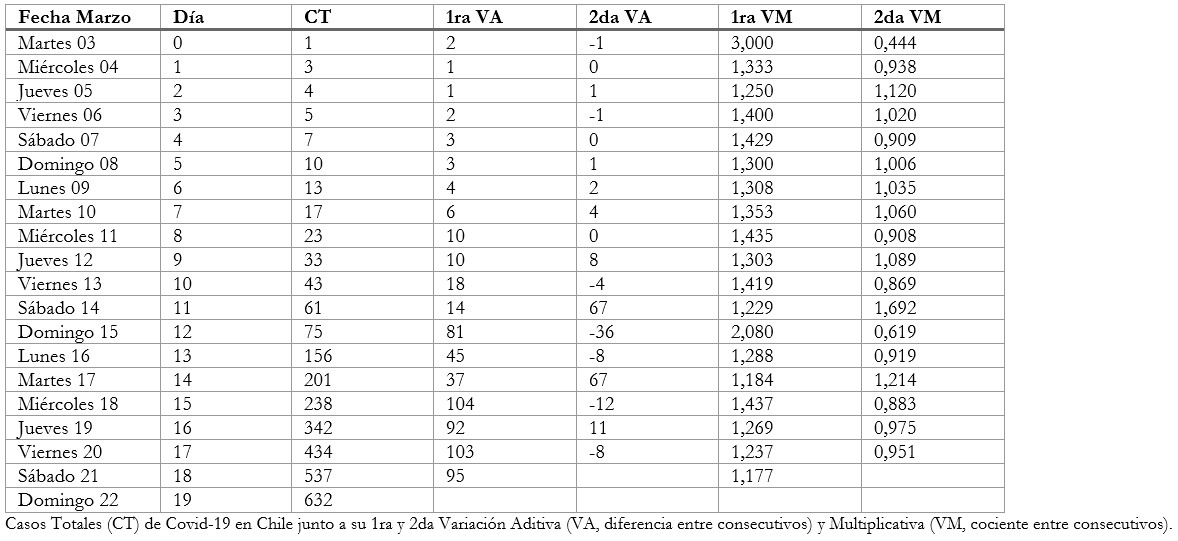
La cantidad de casos totales de COVID-19 en nuestro país a la fecha del reporte (22/03/2020), muestra una clara tendencia al alza formando convexidad. Este comportamiento también es apreciable en su primera variación aditiva (1ra VA, diferencia entre valores consecutivos) y con mayor variabilidad también en la segunda variación aditiva (2da VA, diferencia entre diferencias consecutivas), tal como se muestra desde la tercera a la quinta columna de la Tabla 1 y en la Figura 1 (a)-(c).
 Tamaño completo
Tamaño completo 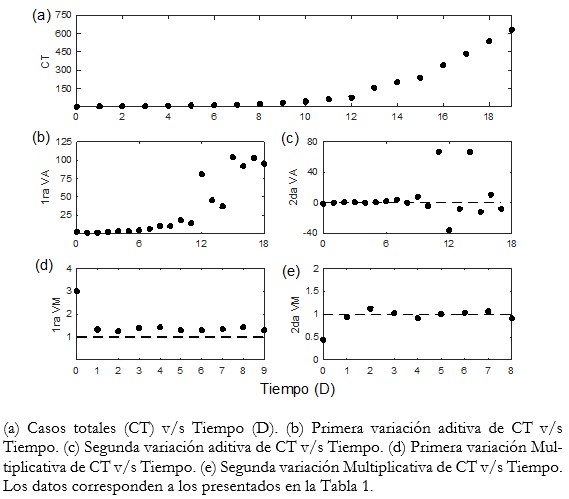 Tamaño completo
Tamaño completo ¿Estamos ante a un crecimiento exponencial? O equivalentemente, ¿los datos conforman una progresión geométrica? Esto es, ¿el nuevo dato es el del día anterior multiplicado por una constante? En general, si no existe mitigación sobre la tasa de contagio, se espera que en una primera fase la curva de casos totales (o acumulada) asemeje a una exponencial, siempre y cuando no existan intervenciones o la disponibilidad de susceptibles es suficiente para significar un freno en la expansión. Asumiendo que existe tal modelo y partiendo desde un primer infeccioso, este posee la forma C(k)=(1+A)k, esto es a modo de ejemplo C(0)=1, C(1)=1+A, C(2)=(1+A)2 y así sucesivamente, donde C son los casos totales, A el incremento porcentual diario y k es el número de días transcurridos desde el caso uno. Notemos que en este modelo la primera variación aditiva será denotada por D(k)≔C(k+1)-C(k)=AC(k), es decir, la misma expresión exponencial (igual base) salvo la constante A. Lo mismo ocurre con la segunda variación aditiva que simbolizamos D2(k), luego D2(k)=D(k+1)-D(k)=A2∙C(k). Por lo tanto, la primera y segunda variación son proporcionales a C(k).
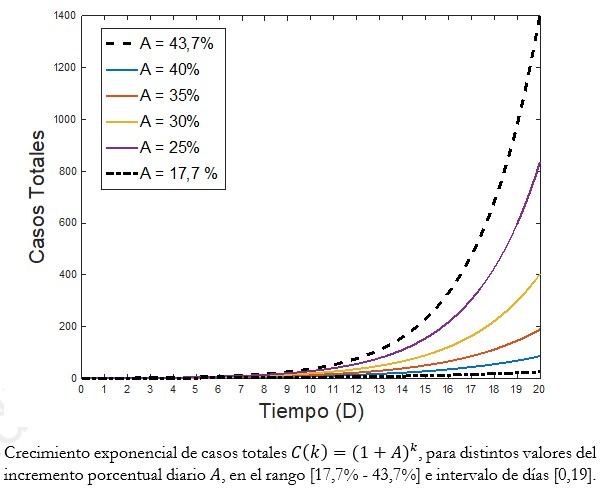
Como ha sido destacado, una propuesta exponencial establece la siguiente relación C(k+1)=(1+A)∙C(k). Luego, realizando una comparación por cociente entre valores consecutivos, nos referimos a la primera y segunda variación multiplicativa, tenemos Q(k)≔C(k+1)/C(k)=1+A y claramente Q2(k):=D(k+1)/D(k)=1. Destacamos que esta tendencia es posible de apreciar en las dos últimas columnas de la Tabla 1. Adicionalmente, exceptuando el primer dato de la Tabla 1, en Chile tenemos un valor de A perteneciente al rango [17,7% (día 18) - 43,7% (día 15)], exceptuando el día 12. En la introducción del COVID-19 en España[8] se observó resistentemente A=20% y en Italia[9] en algún instante se tuvo A=25%.
El actual panorama nacional nos posiciona (a escala temporal equivalente) con cifras iniciales similares a países como Italia y España, siendo este último (desplazado algunos días) catalogado por algunos como la nueva Italia respecto a la rápida propagación del virus. El conocimiento que disponemos respecto a la evolución que ha tenido el COVID-19 en estos y otros países nos brinda la posibilidad de no compartir su realidad epidémica[15]. Cambiar este escenario, solo es posible a través de la implementación de medidas preventivas anticipadas con el potencial de disminuir el incremento porcentual diario (a condición del acatamiento público), pues de lo contario el crecimiento de los casos totales será a ritmos mayores a los deseados (ver Figura 2).
 Tamaño completo
Tamaño completo Proyección cúbica (tasa diaria decreciente)
Los ritmos que muestra la Tabla 1 en conjunto respecto de lo dañino, particularmente en ancianos, que es el COVID-19 en relación a una influenza, nos posicionan en un contexto definitivamente alarmante. Sin embargo, el crecimiento no exponencial no lo es, pues (por lo observado en la sección anterior) esto se reflejaría en la 1ra y 2da VA, y esta última con sus variaciones de signo. Una familia de fácil tratamiento que satisface 2da VM ~ 1, que es el caso, son los polinomios. Ya que, los casos no tienen un crecimiento aritmético y tampoco la 1ra variación aditiva, nos queda la posibilidad de grado tres o más. Se opta por tres por simplicidad y por las comparaciones de la Tabla 2, ya con datos de contagios no importados.
Realizando un escalamiento del tiempo (periodo comprendido entre el 3 y 22 de marzo) y considerando los casos totales (segunda columna de la Tabla 1), a través de la pseudo-inversa de Moore-Penrose[16] obtenemos el ajuste por polinomio cúbico. Así, los casos totales (C) al k-ésimo día, son:
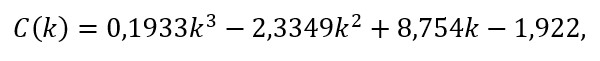
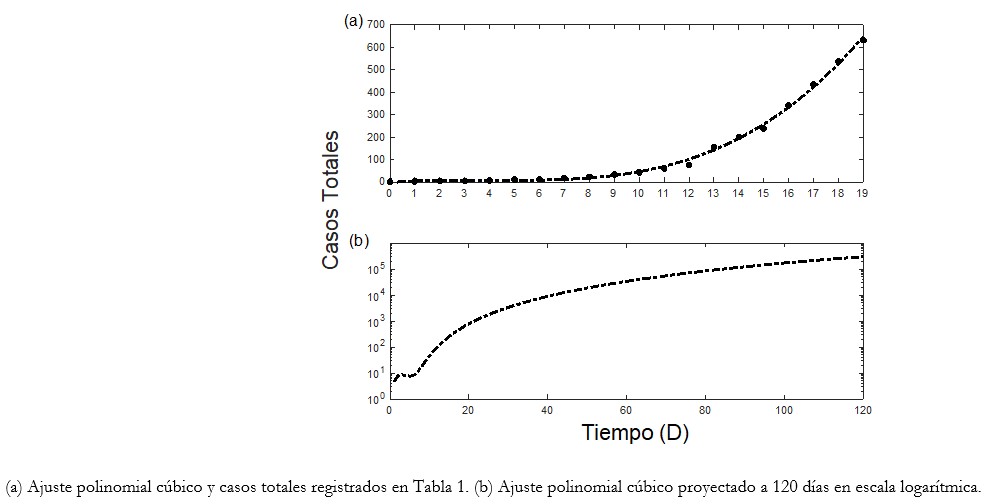
cuya gráfica se muestra en la Figura 3(a), punteando los casos totales registrados. Además, podemos apreciar la estimación numéricamente (aproximando al entero) en la Tabla 2.
 Tamaño completo
Tamaño completo  Tamaño completo
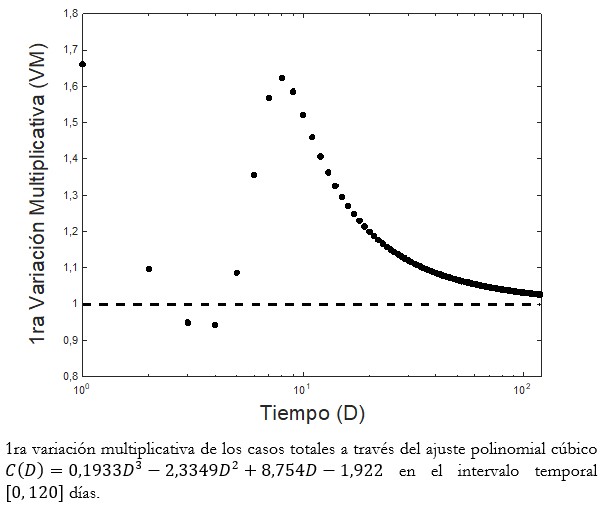
Tamaño completo Mediante este modelo cúbico es posible proyectar la cantidad de casos de COVID-19 a 120 días. El modelo arroja que Chile puede llegar a cifras del orden de 100 000 personas infectadas a finales del mes de junio del presente año (ver Figura 3(b)). Es importante destacar que la proyección realizada no asume algunas condiciones, como las ambientales, por lo que se entiende son similares a las que se han presentado estos primeros días de la enfermedad (un sesgo optimista del modelo). Sin embargo, una observación importante sobre el ajuste polinomial cúbico realizado, es que este asume que la tasa de contagio diaria varía a la baja en el tiempo, que es lo que ocurre cuando existen constantes medidas de mitigación al contagio, que se corresponde con el concepto de aplanar la curva epidémica (los nuevos casos diarios). Lo anterior se puede apreciar en la Figura 4. Esto permite interpretarlo como que el modelo considera que cada día se está realizando un esfuerzo extra, esto es, manteniendo los anteriores y agregando otros más cada día. Una variable epidemiológica como el distanciamiento social, está implícitamente incorporado en este ajuste, como también las medidas que van en la dirección de que los encuentros no se transformen en contactos efectivos.
 Tamaño completo
Tamaño completo Proyecciones exponenciales con control
Cualquiera sea la tasa porcentual (aumento diariamente del total de casos), de prolongarse es, por el geométrico crecimiento que determina, una muy mala noticia. Se requiere controlar, además de realizar sostenidos esfuerzos diarios para ir reduciéndola. Ahora, con el fin de construir distintos escenarios que representen mencionado esfuerzo introducimos un modelo de tasa variable para los casos totales del tipo:
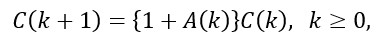
con lo que, asumiendo C(0)=1, tenemos:
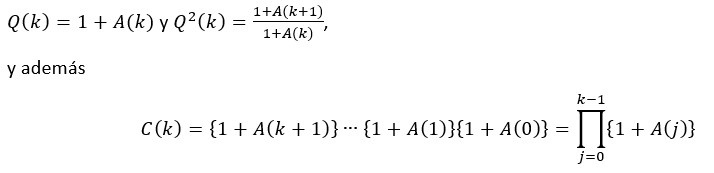
Notemos que para frenar el crecimiento de los casos totales se requiere D2C(k)<1, esto equivale a A(k+1)
Por ejemplo, si asumiéramos que la relación entre tasas porcentuales diarias y entre días consecutivos (k y k+1) está definida por la siguiente recurrencia:
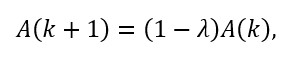
Siendo λ ϵ (0,1) el factor (o fracción) en que los esfuerzos de control logran reducir dicha tasa diaria. De este modo, en un despeje elemental por reiteración, tenemos A(k)=(1-λ)kA(0), y luego
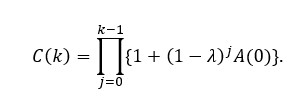
Respecto de la curva de los nuevos casos diarios, los cálculos que apartamos al Apéndice, nos dicen que:
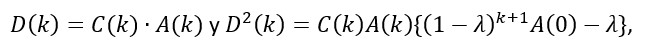
Para todo k≥0. Así, la condición sobre (k,λ), esto es, la relación día-factor de esfuerzo para lograr bajar el número de nuevos infectados es (condición de control):
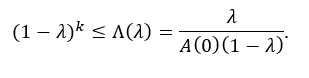
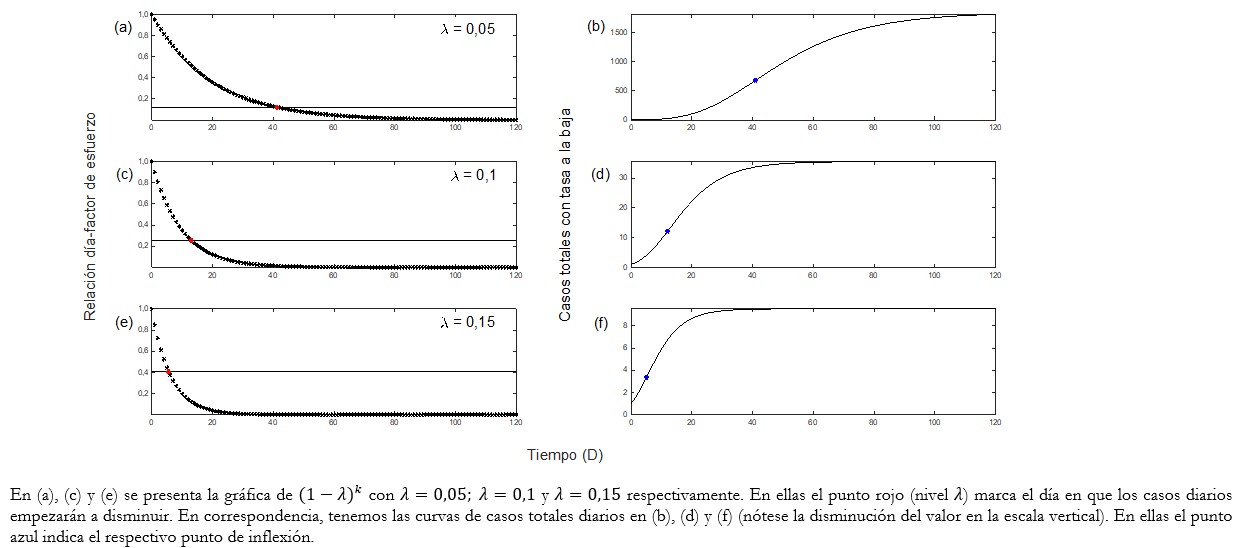
En las gráficas de la Figura 5 (a), (c) y (e) se ha graficado para tres valores de λ en {5%, 10%, 15%}, la función exponencial (1-λ)k variando k. Notemos que la recta horizontal que atraviesa la curva corresponde al umbral Λ(λ). Así, el punto en rojo marca el instante (día) en que los nuevos casos diarios comienzan a disminuir. En las gráficas de la Figura 5 (b), (d) y (f), se representan los casos totales, en ellas se marca en azul los puntos de inflexión (asociados con los en rojo). Como es de esperar un mayor parámetro de esfuerzo λ, disminuye el tiempo de máximo crecimiento k.
 Tamaño completo
Tamaño completo Notemos que, en la práctica, con la epidemia transcurriendo ya el k-ésimo día y conociendo solo los valores de los casos totales pasados, ¿cuál es el valor del parámetro de esfuerzo ejercido el día anterior? Por la expresión de C(k) en términos de λ, se deduce que (condición de testeo):
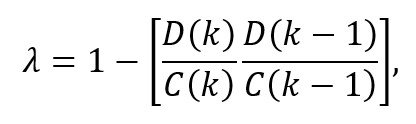
es decir, uno menos el cociente entre los dos últimos porcentajes de crecimiento de los casos. El valor testeado se puede remplazar en la condición de control para chequear si se deben incrementar aún más los esfuerzos ya desplegados.
Conclusiones
Si ante un virus (pandémico) circulando no hay reacción, ni siquiera con el intento de acciones que puedan mitigar, necesariamente los ritmos de crecimiento de los casos serán geométricos, con duplicación en muy pocos días. ¿Qué se puede oponer a una progresión geométrica para forzarla a declinar? No pueden ser acciones que en la práctica tengan el potencial de reducir una determinada cota de casos diarios. La matemática nos dice que no se amortigua un ritmo geométrico con uno aritmético. En consecuencia, el camino para controlar la pandemia es imponerle el contrario, digamos confrontar con un accionar que también tenga potencial geométrico pero inverso (a la baja) y necesariamente superior, y esto es lo que con el parámetro λ hemos querido representar. ¿Cuál es la tasa mínima que dicho ritmo de esfuerzo debe tener para frenar el de propagación? Es lo que responde la condición paramétrica umbral presentada en este artículo.
En lo práctico, se trata de formar una secuencia diaria de medidas unas sobre otras. Si un día se implementa una acción sobre la población, esta debe tener la propiedad de no perder su efecto reducidor y, además, al día siguiente, agregar nuevas acciones sin retirar las existentes para que tengan igual o superior efecto amortiguador. Sin embargo, no se está seguro de que al implementar esta secuencia se alcance el umbral deseado. Si bien reduce la propagación, sigue persistiendo la interrogante de si será lo suficiente para la meta esperada. ¿En qué porcentaje las medidas reducen la tasa de contagio diaria? ¿En qué orden óptimo han de ser implementadas medidas como cuarentena a casos sospechosos, teletrabajo, toque de queda, cierre de fronteras terrestres y áreas, y vacunación contra la influenza a la población en riesgo? Esto no es algo que se pueda responder dentro del alcance de este artículo, sino que constituye materia de futuras investigaciones cuando la experiencia se concrete. La secuencia de acción debe continuar día a día, no se puede detener. Se debe asegurar el efecto sostenido de cada acción y se debe conocer cómo se asegura su efecto, cuántas y cuáles otras medidas de mitigación más se deben incorporar. Todo esto es un gran desafío. En el curso de las acciones, destaquemos que la observación de las cifras y los patrones que exhiban del proceso en curso es clave. ¿Hay evidencia de un porcentaje sostenido de reducción de la tasa de contagio diaria? ¿Sí o no? Ante un no, con todos sus costos, la estrategia de supresión podría ser “el” camino.
Cerramos este artículo con fecha 22/03/2020. En Chile la tasa porcentual de incremento ha sido 17,7% y acumula un cuarto día a la baja y es el deseo que se sostenga, después del domingo anterior que marcó un 108%. Muy pronto se cumplirá una semana desde que en Chile el Ministerio de Salud informó el paso a fase 4 en cuanto a medidas de mitigación[17] y aumentan las restricciones al movimiento para lograr distanciamiento. Una estrategia para aplanar la curva de nuevos casos tempranamente requiere de enormes esfuerzos diarios para lograrlo, de algún modo no del todo precisado en este artículo, pero representado en el parámetro λ. Debemos aprender las lecciones que nos deja el contexto internacional para saber cómo la situación de Europa (Italia y España) no se convierta en el mañana de Chile.
Apendice
Condición de control
Notemos que la igualdad D(k)=C(k)∙A(k) es inmediata y como D2(k)=D(k+1)-D(k)=C(k+1)A(k+1)-C(k)A(k), tenemos que D2(k) es iguala {(1+A(k))A(k+1)-A(k)}C(k). Entonces, usando que A(k+1)=(1-λ)A(k) se llega a
D2(k)={(1-λ)A(k)-λ}C(k)A(k),
desde donde D2(k)≤0, toma la forma (1-λ)k≤Λ enunciada.

