Análisis
← vista completaPublicado el 15 de mayo de 2020 | http://doi.org/10.5867/medwave.2020.04.7898
Proyección epidemiológica de COVID-19 en Chile basado en el modelo SEIR generalizado y el concepto de recuperado
An epidemiological forecast of COVID-19 in Chile based on the generalized SEIR model and the concept of recovered
Resumen
La pandemia de COVID-19 declarada por la Organización Mundial de la Salud (OMS) ha generado un amplio debate respecto de las proyecciones epidemiológicas que tendrá a nivel global en nuestro planeta. Con los datos obtenidos del Ministerio de Salud de Chile (MINSAL), se efectuó un estudio prospectivo utilizando un modelo SEIR (Susceptible-Expuesto-Infectado-Recuperado) generalizado con el objetivo de estimar la evolución del COVID-19 en Chile. La estimación se realizó bajo tres escenarios con datos oficiales del Ministerio de Salud: escenario 1 solo con datos oficiales; escenario 2 se añade el criterio de recuperados propuesto por organizaciones internacionales de salud y escenario 3 se incorpora el criterio de recuperados propuesto por organizaciones internacionales de salud, sin considerar fallecidos en el total de recuperados. Existen diferencias considerables entre el escenario 1 en comparación al 2 y 3 en número de fallecidos, enfermos activos y duración de la enfermedad. El escenario 3, considerado el más adverso, estima un total de 11 000 personas contagiadas, 1151 fallecidos y que el máximo de la enfermedad ocurriría durante los primeros días de mayo. Se concluye que el concepto de “recuperado” puede ser decisivo para las proyecciones epidemiológicas de COVID-19 en Chile.
Ideas clave
- Las proyecciones epidemiológicas utilizando el modelo matemático Susceptible-Expuesto-Infectado-Recuperado han permitido establecer estrategias para minimizar los efectos del virus.
- En Chile, se produjo controversia respecto al concepto de recuperado dictaminado por las autoridades sanitarias.
- No existen para Chile estudios de proyección epidemiológica utilizando el modelo Susceptible-Expuesto-Infectado-Recuperado con los datos oficiales del Ministerio de Salud. Los resultados de este estudio vinculan el concepto de recuperados y las estimaciones en tres escenarios, contribuyendo en la discusión respecto a considerar los criterios de recuperación sugeridos por organismos internacionales y en la comprensión de la magnitud del COVID-19 en Chile.
- Las limitaciones del estudio se relacionan a las propias de los modelos matemáticos y al tamaño y confiabilidad de los datos oficiales del Ministerio de Salud.
Introducción
El SARS-CoV-2, responsable de la enfermedad llamada por la Organización Mundial de la Salud como COVID-19, es un virus que pertenece a la familia Coronaviridae de ácido ribonucleico (ARN) monocatenario[1]. Desde una perspectiva virológica, ha presentado múltiples mutaciones entre las que se encuentran la nueva cepa de COVID-19. Este evento sanitario se originó en Wuhan, China en diciembre de 2019 y se sospecha que su propagación se debió a una zoonosis entre murciélagos, un animal indeterminado como vector y humanos[2].
Los síntomas de una persona con COVID-19 son fiebre, cefalea, odinofagia, disnea, mialgia y tos[2]. El virus tiene un periodo de incubación de 5,2 días y un R0 de 2,24 a 3,58 en países donde se ha estudiado[3]. A nivel mundial hasta el 13 de abril de 2020, el COVID-19 ha infectado a 1 970 225 personas, 124 544 fallecimientos a causa de este virus y una tasa de letalidad del 5,4% dependiendo de la localización geográfica, del porcentaje de población adulta mayor, de las respuestas de los servicios de salud y de otras variables que aún no son analizadas[4]. A pesar de tener una baja letalidad, el COVID-19 presenta un contagio de dos a 2,5 veces mayor en comparación a la influenza[5]. Una de las medidas más ampliamente utilizada ha sido el aislamiento social, generando una contracción económica mundial y una alta demanda de los servicios de salud para las poblaciones afectadas[6].
En Chile, este evento ha sido monitorizado desde el 3 de marzo de 2020, cuando se notificó la primera persona contagiada de COVID-19. A la fecha, 12 de abril de 2020, el Ministerio de Salud (MINSAL) ha reportado 7525 personas contagiadas y 82 fallecidos, concentrando la mayor cantidad de casos en las regiones Metropolitana, Araucanía, Biobío y Ñuble[7]. En relación con los casos recuperados, existe controversia debido al criterio utilizado por el Ministerio de Salud, el cual establece como “recuperado” a toda persona que cumpla 14 días desde la confirmación para examen de COVID-19, no presente síntomas y se encuentre en buenas condiciones de salud[8].
No obstante, este criterio va en contraposición a lo determinado por la Organización Mundial de la Salud, el Centro de Control y prevención de enfermedades (CDC), y al Centro Europeo para la Prevención y Control de Enfermedades (ECDC)[9],[10],[11],[12]. En la Tabla 1 se detallan las recomendaciones internacionales para dar por recuperada a una persona con diagnóstico positivo de COVID-19.
 Tamaño completo
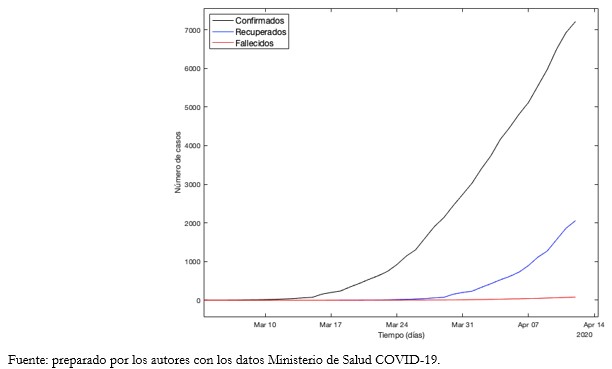
Tamaño completo Hasta el 12 de abril de 2020, Chile presentó 2059 casos recuperados de COVID-19[7]. En el Gráfico 1 se observan las cifras oficiales de COVID-19 en Chile desde el 3 de marzo 2020.
 Tamaño completo
Tamaño completo Por otra parte, los reportes entregados por el Ministerio de Salud incluyen a fallecidos en el total de recuperados[13], situación que no es contemplada por las directrices internacionales, las cuales indican el estado de “fallecido” no es homologable al estado de “recuperado”[13].
Debido al comportamiento del virus, particularmente en China, Italia y España; se hace necesario contar con proyecciones que puedan estimar la magnitud del evento. En esa dirección, cobra importancia la utilización de modelos matemáticos que, en este tipo de casos, posibiliten acciones anticipadas para evitar la propagación del agente viral y favorecer la toma de decisiones por parte de las autoridades. Es importante mencionar que los modelos matemáticos brindan pronósticos y se utilizan para comprender los procesos epidémicos en pos de generar estrategias para disminuir su diseminación. Los modelos matemáticos en salud han sido utilizados desde las primeras aproximaciones de Daniel Bernoulli con la epidemia de la peste durante el siglo XVII[14]. Posteriormente, modelos epidemiológicos predictivos deterministas fueron utilizados según las características del agente etiológico[14]. En la Tabla 2 se explican algunos modelos matemáticos utilizados en epidemiología.
 Tamaño completo
Tamaño completo Uno de los modelos utilizados para esta emergencia ha sido el Susceptible-Expuesto-Infectado-Recuperado (SEIR). Este modelo es una adaptación al modelo Susceptible, Infectado y Recuperado (SIR) propuesto por Kermack y Mc Kendrick en 1927[15]. Dicho modelo matemático busca conocer la evolución de una epidemia considerando a los sujetos susceptibles, expuestos, infectados y recuperados. Una propuesta de generalización del clásico modelo Susceptible-Expuesto-Infectado-Recuperado ha sido publicada por Peng y colaboradores[16], incorporando básicamente la categoría “cuarentenado” a las ya existentes “susceptible”, “expuesto”, “infectado” y “recuperado”. Estudios efectuados recientemente han demostrado que el modelo Susceptible-Expuesto-Infectado-Recuperado se ajusta a la evolución que ha tenido la enfermedad en los países afectados[17],[18],[19].
Resulta relevante, por tanto, conocer la proyección epidemiológica de COVID-19 en Chile debido a la alta incidencia de la enfermedad en comparación a otros países de la región[4], y ser una de las naciones perteneciente a la Organización para la Cooperación y Desarrollo Económicos (OCDE) con menor capacidad de respuesta hospitalaria al contar con 2,1 camas por cada mil habitantes[20].
En Chile, la utilización de modelos matemáticos se ha enfocado en las proyecciones epidemiológicas con ajuste cúbico, dando como resultado una estimación de 100 000 personas afectadas de COVID-19 hasta julio de 2020[21], mientras otro estudio ha estimado la reducción de la tasa de contagios para evitar el colapso hospitalario en el país[22]. No obstante, no se han hallado investigaciones de este tipo con el empleo del modelo Susceptible-Expuesto-Infectado-Recuperado en Chile.
En consecuencia, el objetivo de este estudio es estimar, mediante el uso del modelo Susceptible-Expuesto-Infectado-Recuperado generalizado, la proyección epidemiológica del COVID-19 en Chile en tres escenarios con los datos oficiales del Ministerio de Salud. Los escenarios contemplan los criterios de recuperados del Ministerio de Salud, las consideraciones internacionales de recuperación y los fallecidos eliminados del total de recuperados.
Metodología
Modelo Susceptible-Expuesto-Infectado-Recuperado generalizado
La presente investigación secundaria utiliza la propuesta de generalización del modelo Susceptible-Expuesto-Infectado-Recuperado descrita por Peng y colaboradores[16], la cual detalla los siguientes estados en el tiempo t:
- S(t), el número de casos susceptibles.
- P(t), el número de casos no susceptibles: son aquellos que se han protegido y no contraen la enfermedad.
- E(t), el número de casos expuestos: son aquellos infectados, pero aún no son infecciosos, es decir que no contagian. Permiten considerar el periodo de incubación de una enfermedad (o periodo de latencia).
- I(t), el número de casos infectados: son aquellos que pueden infectar a otros y no están en cuarentena.
- Q(t), el número de casos en cuarentena: quienes son positivo a la enfermedad y han sido puestos en una condición que imposibilita infectar a otros.
- R(t), el número de casos recuperados o curados.
- D(t), el número de casos fallecidos.
En consecuencia, se obtiene que S(t) + P(t) + E(t) + I(t) + Q(t) + R(t) + D(t) = N, donde N es el total de la población en cierta región o país.
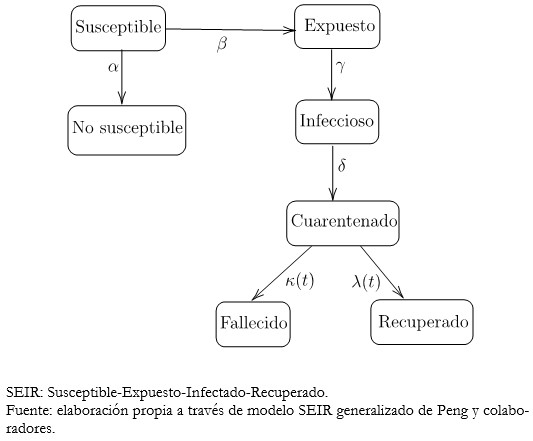
La relación entre los diferentes estados es dada en la siguiente representación (Figura 1), donde los coeficientes {𝛼,𝛽,𝛾−1,𝛿−1,𝜆(𝑡),𝜅(𝑡)} representan la tasa de protección, la tasa de infección, el promedio de tiempo latente, el promedio de tiempo en cuarentena, la tasa de recuperación y la tasa de mortalidad respectivamente. Se observa que la tasa de recuperación y mortalidad dependen de tiempo t[16].
 Tamaño completo
Tamaño completo Además, la dinámica del modelo está dada por el siguiente sistema de ecuaciones diferenciales:
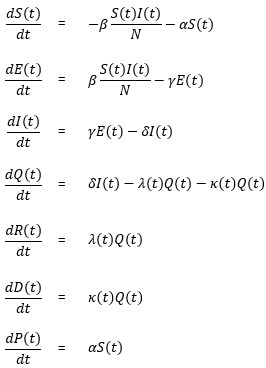
Más aún, es posible reescribir el sistema anterior en forma matricial:
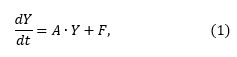
donde Y = (S,E,I,Q,R,D,P)T y
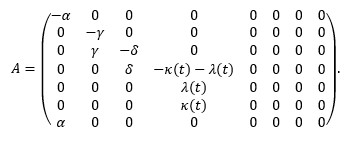
Finalmente, el número básico de reproducción (R0) del virus es gobernado en el tiempo t por la ecuación:
R0(t)=βδ-1(1-α)t.
Estimación de parámetros
El modelo de ecuaciones fue implementado usando el código para MATLAB disponible en Matlab File Exchange (https://it.mathworks.com/matlabcentral/fileexchange/74545-generalized-seirepidemic-model-fitting-and-computation)[23].
Los datos son extraídos desde una tabla con la información oficial que el Ministerio de Salud entrega en su sitio web[7]. La tabla está compuesta por los datos de número de casos confirmados (Q), recuperados (R) y fallecidos (D). Los datos Q, R y D representan los supuestos iniciales, y α,β,γ,δ,λ y κ son los coeficientes para estimar con las variables de estado iniciales para casos infectados y expuesto {E0,I0}. Para la modelación, las condiciones iniciales se dan como primer estimado. Luego, los valores se calculan siguiendo un enfoque de ajuste de curva de mínimos cuadrados que considera los datos observados (Q, R, D) en el tiempo. La ecuación (1) se resuelve utilizando el método Runge-Kutta de cuarto orden, debido a que es una ecuación no lineal y para la cual no existe una solución explícita. El método Runge-Kutta de cuarto orden es usado por su velocidad de convergencia. El error por iteración es menor que el incremento de dos puntos sucesivos elevado a 5, mientras que el error total acumulado es menor que el incremento elevado a 4. Es decir, tiene una velocidad de convergencia de orden 4. Por esta razón es usado en métodos computacionales[24].
Como λ y κ dependen del tiempo, Peng y colaboradores sugieren una evolución exponencial de los dos parámetros[16]. Aquí se restringen λ y κ para que se ajusten con una tendencia exponencial explícitas dependientes del tiempo. La idea detrás de esta dependencia es que la tasa de mortalidad a causa de la enfermedad debería ser cero después de un tiempo infinito. Si la tasa de mortalidad se mantiene constante, el número de muertes puede sobreestimarse. Al mismo tiempo, la tasa de recuperación también está aumentando hacia un valor límite.
Resultados
A partir de la información que ha entregado el Ministerio de Salud respecto de la clasificación de recuperados desde el 3 de marzo al 12 de abril[7] de 2020 y los criterios internacionales de personas recuperadas de COVID-19[9],[10],[11],[12], presentamos tres escenarios posibles modelados con Susceptible-Expuesto-Infectado-Recuperado generalizado:
a. Escenario 1: aplicado con los datos oficiales entregados por el Ministerio de Salud. En este escenario se utilizó el número de recuperados totales con el criterio establecido por dicha cartera (14 días después de dar positivo al examen de COVID-19).
b. Escenario 2: aplicado con los datos oficiales, considerando protocolo de recuperación de 28 días. Este escenario contempla el criterio de recuperación propuesto por la Organización Mundial de la Salud y Centro Europeo para la Prevención y Control de Enfermedades, a saber: 14 días de evolución sin síntomas, dos exámenes negativos de COVID-19 con al menos 24 horas de diferencia y 14 días adicionales de cuarentena. En consecuencia, se contemplan 28 días de recuperación.
c. Escenario 3: aplicación con los datos oficiales, considerando protocolo de 28 días de recuperación y excluyendo a los fallecidos del total de recuperados. Para este contexto se utilizaron los criterios del escenario 2, pero sin contabilizar a los fallecidos en el total de recuperados[13].
Para todos los escenarios proyectados se calcularon los siguientes indicadores en la ventana temporal del 3 de marzo al 12 de abril:
- Total de infectados: número total acumulado de personas infectadas por COVID-19.
- Máximo de enfermos activos: mayor cantidad de personas con infección activa de COVID-19 y en cuarentena.
- Día estimado recuperados mayor a infectados: fecha aproximada donde la cantidad acumulada de recuperados es mayor a las personas infectadas activas y en cuarentena.
- Total de fallecidos: número acumulado de personas muertas por COVID-19.
- Estimación de R0: aproximación de R0 durante el evento de COVID-19.
Es importante mencionar que los parámetros de ajuste de cada escenario se obtuvieron mediante el método de mínimos cuadrados que establece el Software anteriormente mencionado.
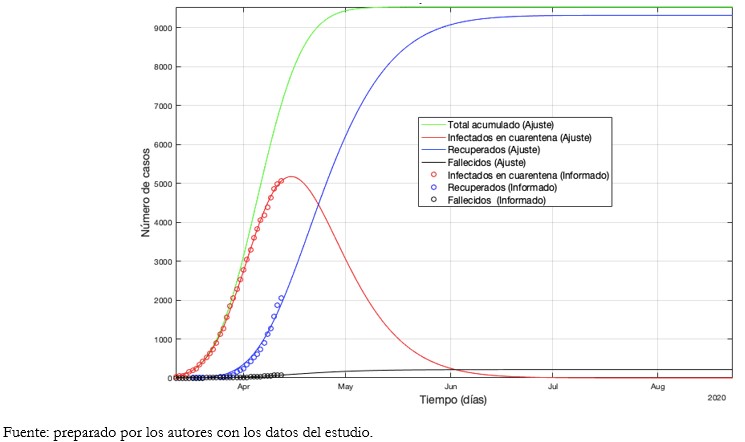 Tamaño completo
Tamaño completo 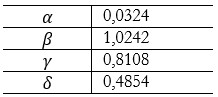 Tamaño completo
Tamaño completo De acuerdo con la proyección del Gráfico 2, se estima un total de 9536 casos acumulados de COVID-19 para el 7 de junio. El máximo de enfermos activos ocurriría aproximadamente el 15 de abril con un total de 5177 casos. A partir del 23 de abril, la cantidad de recuperados acumulados sería mayor a los enfermos activos. En la misma fecha, el total de infectados disminuiría de forma sostenida hasta el 7 de mayo. Los fallecidos ascenderán a 210 muertos por causa de COVID-19. Se estimó para este escenario un R0 de 2,1098. En el Gráfico 3 se evidencia R0 menor a 1 alrededor del 3 de abril.
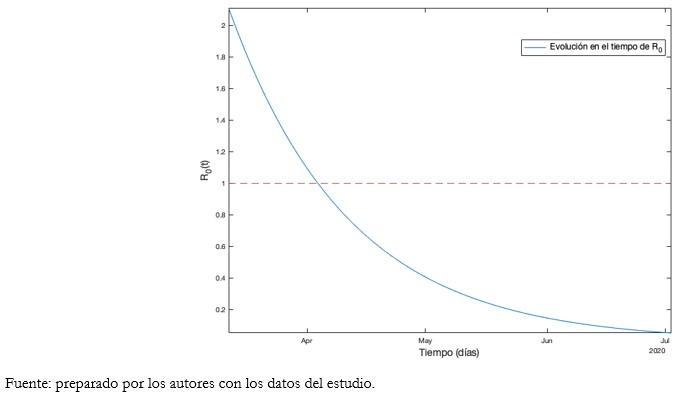 Tamaño completo
Tamaño completo En ese sentido, al ser R0 mayor a 1 hasta el 3 de abril, la curva de expuestos más infectados alcanzaría su máximo para dicha fecha.
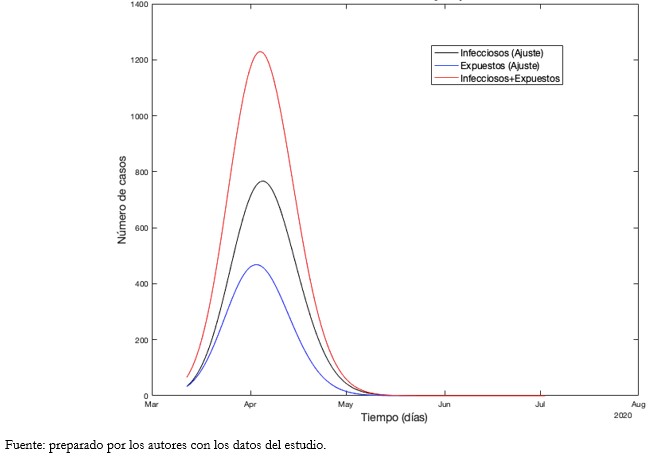 Tamaño completo
Tamaño completo 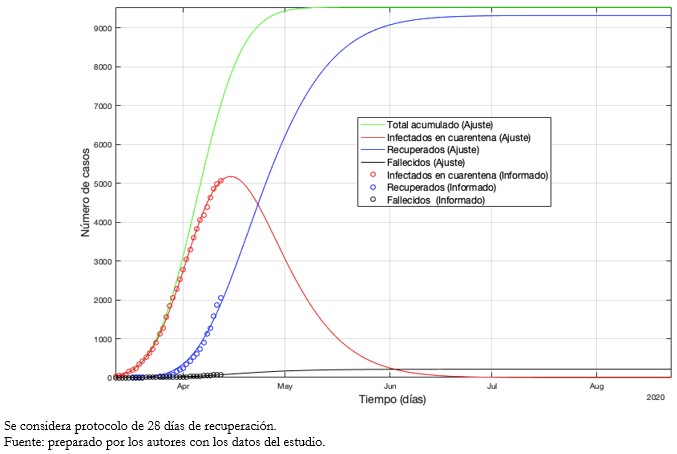 Tamaño completo
Tamaño completo 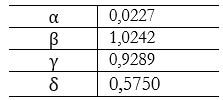 Tamaño completo
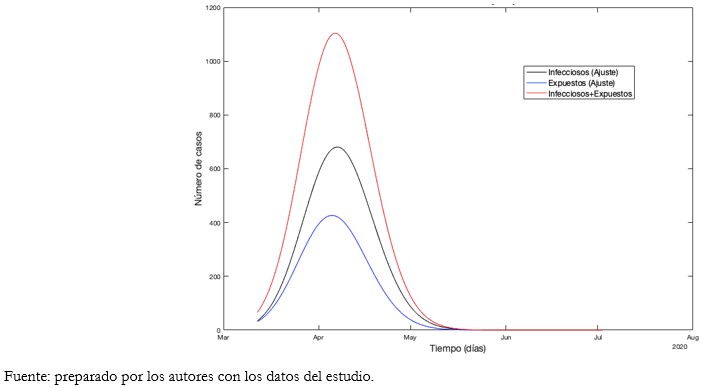
Tamaño completo Según el Gráfico 5, representativo del escenario 2 propuesto, se estima un total de 11 000 personas infectadas acumuladas hasta el 10 de agosto. La estabilización de la curva de infectados se lograría a partir del 1 de mayo y, posteriormente, el 12 del mismo mes. El máximo de enfermos activos ocurriría desde el 30 de abril con 9872 casos. Los casos recuperados serían mayores a los infectados activos para el 6 de agosto. Los fallecidos, hasta el 10 de agosto, ascenderían a 1004 personas. El R0 estimado es de 1,7812.
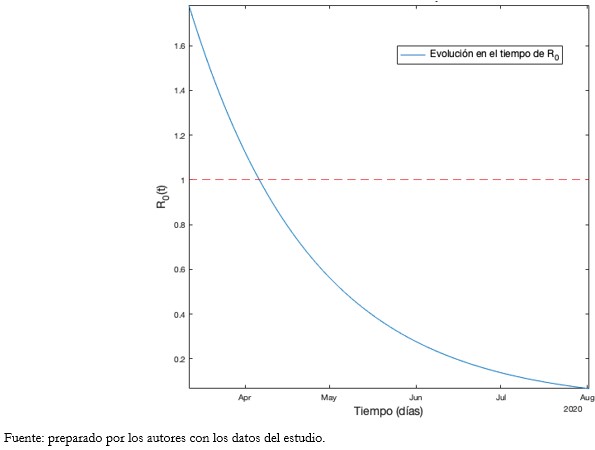 Tamaño completo
Tamaño completo El R0 sería mayor a 1 hasta el 6 de abril. Por ello, la curva de expuestos más infectados alcanzaría su máximo para el mismo día.
 Tamaño completo
Tamaño completo  Tamaño completo
Tamaño completo 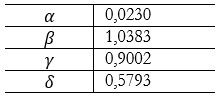 Tamaño completo
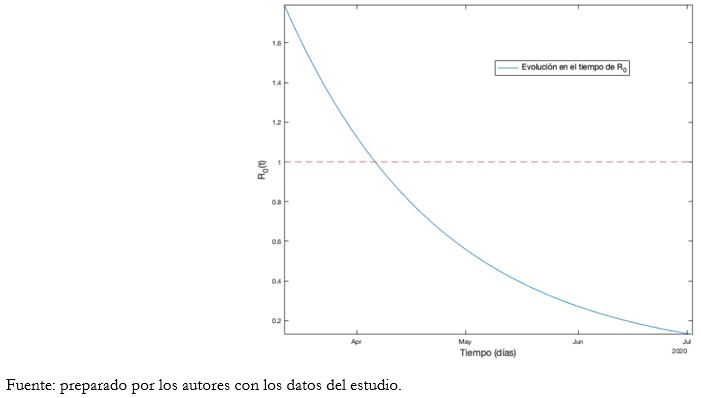
Tamaño completo Según la proyección del Gráfico 8, acorde al escenario 3 propuesto, se estima en cerca de 11 000 los infectados acumulados hasta el 10 de agosto. La estabilización de la curva de infectados ocurriría el 1 de mayo y luego el 12 del mismo mes. Se prevé que el máximo de enfermos activos para el 1 de mayo con 9944 casos. Desde el 3 de septiembre se notificaría la mayor cantidad de recuperados en relación con los infectados activos. El total de fallecidos, para el 31 de agosto, alcanzaría un total de 1151 muertes a causa del COVID-19. El R0 se aproxima a 1,7923.
 Tamaño completo
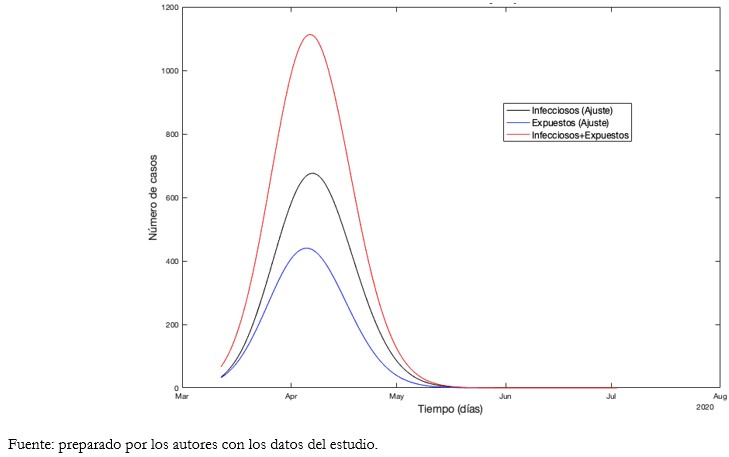
Tamaño completo El máximo de expuestos e infectados se estima para el día 6 de abril. Esto se explica ya que R0 es mayor a 1 hasta dicha fecha.
 Tamaño completo
Tamaño completo Comparación de los escenarios
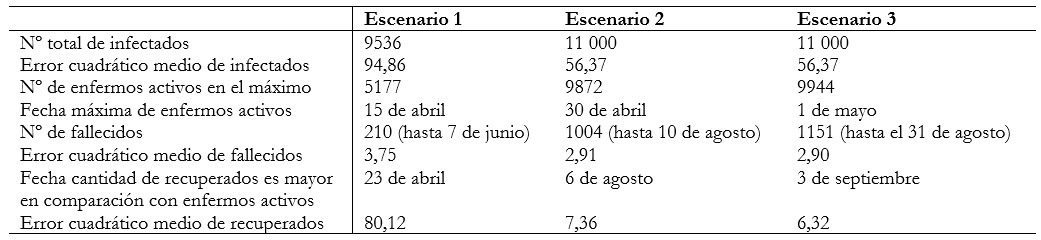
Los tres escenarios propuestos son proyecciones basadas en los datos oficiales del Ministerio de Salud hasta el 12 de abril de 2020. Las diferencias en cuanto al número total de infectados, máximo de enfermos activos y número de fallecidos se asociaron con los criterios utilizados por la autoridad sanitaria para decretar las personas afectadas de COVID-19 como recuperadas y la contabilización de los fallecidos en el reporte de recuperados.
 Tamaño completo
Tamaño completo Discusión
Los informes epidemiológicos del Ministerio de Salud, disponibles en su sitio web, tienen por objetivo entregar información actualizada sobre la situación de COVID-19 en Chile de manera regular. En estos documentos se precisan una serie de conceptos clave, por ejemplo, caso notificado, caso confirmado, entre otros. Llama la atención que el concepto de “caso recuperado” no sea explicitado en un documento oficial, ya que es fundamental a la hora de estudiar el comportamiento de cualquier enfermedad. En ese sentido permanece la incertidumbre, en la sociedad y en el mundo académico, respecto a la decisión de considerar a las personas fallecidas como recuperadas, como también la no inclusión de las recomendaciones de recuperación de COVID-19 emanadas por prestigiosas instituciones internacionales de salud. Dicha incertidumbre ha sido ampliada por expertas/os y colegios profesionales, quienes señalan su preocupación por los elementos anteriormente señalados, adicionando dudas empíricas respecto al subdiagnóstico a causa de la baja tasa de pruebas y a los escasos datos epidemiológicos comunales[25]. Si esa situación es cierta, existen bajas probabilidades de aportar en la comprensión del COVID-19 en Chile mediante modelos matemáticos, tensionando las proyecciones comunicadas por las autoridades de gobierno. Esto último refuerza la idea de establecer un sistema de monitoreo epidemiológico consistente y confiable. Sin ello y con la anulación de medidas de prevención de contagio del virus, aumenta la probabilidad desarrollar nuevos máximos de la enfermedad durante los siguientes meses[26].
En lo que respecta al concepto de recuperados, es relevante mencionar que dicha nomenclatura se encuentra presente en la mayoría de los modelos deterministas basados en Susceptible, Infectado y Recuperado, por lo que su incorporación vuelve al modelo más complejo[27]. En el caso del modelo Susceptible-Expuesto-Infectado-Recuperado generalizado, el cual distingue en dos categorías distintas a los recuperados y fallecidos, resulta evidente la inconsistencia de los datos y, por consiguiente, un inadecuado ajuste al modelo propuesto por Peng y colaboradores[16].
En efecto, de acuerdo con los datos entregados por el Ministerio de Salud y a la modelación con una generalización de Susceptible-Expuesto-Infectado-Recuperado en tres escenarios, existe una gran variabilidad de los resultados, siendo alarmante la diferencia en la proyección de fallecidos (210 para el escenario 1 y 1151 para el escenario 3), la cantidad de enfermos activos (5177 en el escenario 1 y más de 9000 en los otros dos). Esto último hace suponer una posible sobrecarga del sistema de salud, particularmente debido a las sustanciales discrepancias entre el escenario 1 en comparación con 2 y 3.
Sumado a lo anterior, se observa una diferencia de al menos 15 días en el máximo de enfermos activos entre los escenarios anteriormente expuestos. Este dato es relevante para la planificación de los cuidados preventivos y curativos en el contexto del COVID-19. En consecuencia, ajustes al concepto de recuperados efectuados en el escenario 2 y 3 permiten obtener pronósticos con un mejor ajuste y en corto tiempo, siendo congruentes con las proyecciones realizadas en China, España e Italia[26],[28],[29].
Las diferencias en las proyecciones de fallecidos son, a nuestro juicio, considerables y lleva a reflexionar que la variable “recuperados” interviene en esta disimilitud. Con el propósito de esclarecer esta situación, se efectuaron simulaciones de casos recuperados con valores intermedios entre los escenarios 1 y 2, tal como se observa en el Gráfico 11. Se denominaron a los valores intermedios, simulaciones uno, dos, tres y cuatro.
 Tamaño completo
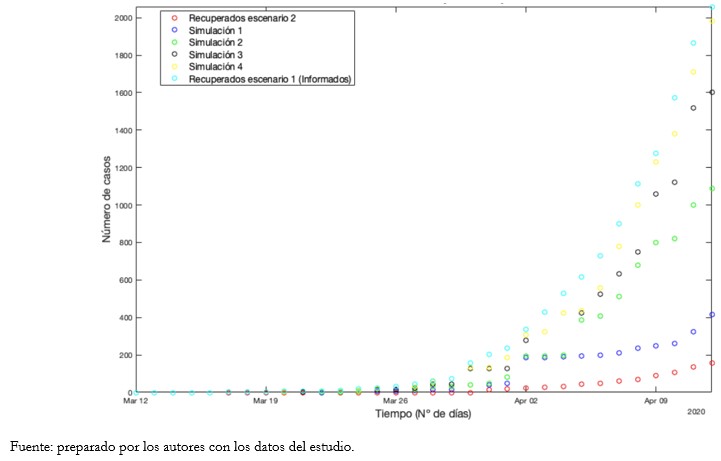
Tamaño completo Asimismo, se realizaron ajustes considerando los mismos casos confirmados-fallecidos y se modificó la variable “recuperados”. En el Gráfico 12 se evidencian las diferencias en proyecciones de curvas ajustadas para recuperados.
 Tamaño completo
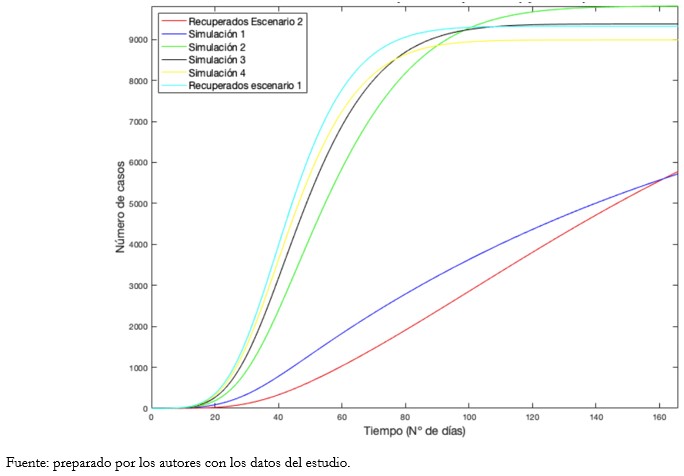
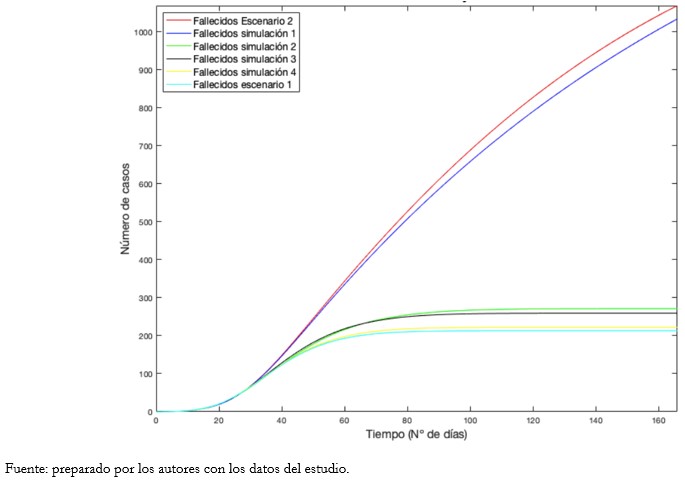
Tamaño completo Finalmente, también se obtuvo la curva de fallecidos para cada caso de recuperados descrita en el Gráfico 13.
 Tamaño completo
Tamaño completo En síntesis, comparando los Gráficos 12 y 13, en la medida que la velocidad de la curva de recuperados aumenta (escenario 1), la de fallecidos tiende a aplanarse, existiendo una aparente relación inversa entre estas estimaciones. Por lo tanto, el establecimiento de los criterios de recuperación tiene un impacto en las proyecciones epidemiológicas de COVID-19. Como supuesto, resultaría prudente establecer criterios de recuperación basados en la evidencia científica recopilada por organizaciones internacionales de salud, dotándolo de mayor validez en el contexto del uso de modelos matemáticos predictivos. Esto último se sostiene por el menor error cuadrático obtenido en los escenarios 2 y 3 en comparación al 1 (Tabla 6).
Otro elemento importante es la duración del evento. En el escenario 1 se estima la finalización del brote epidémico durante la primera semana de junio. Sin embargo, en las otras dos situaciones, se prevé para la segunda mitad de agosto o comienzo de septiembre. Esta diferencia puede resultar sustancial en cuanto a establecer medidas de normalización como retorno a clases de estudiantes de enseñanza básica, media y universitaria, reactivación económica, aportes a las familias vulnerables, retorno al empleo, planificación de cuarentenas, entre otras acciones.
Limitaciones
Una de las limitaciones de este estudio es el desconocido comportamiento del agente patógeno y el impacto de las medidas de salud pública adoptadas para evitar su propagación. En palabras de Rojas-Vallejos, el foco de atención debe estar en los supuestos subyacentes involucrados en el modelo y no en la estimación propiamente tal[30]. En ese sentido, el autor señala que para comprender la pandemia de COVID-19 desde una perspectiva matemática-epidemiológica, se debe contar con varios modelos y escenarios.
De la misma forma, otras limitaciones se asociaron al tamaño y confiabilidad de los datos oficiales obtenidos hasta el 12 de abril. En relación con el tamaño de la muestra, al contar con un conjunto de datos de magnitud reducida, resulta dificultoso estimar con precisión la proyección epidemiológica de COVID-19 en Chile. Respecto a la confiablidad de los datos, se ha conocido públicamente el retraso en los resultados de examen de COVID-19[31] y la situación descrita anteriormente en cuanto a los criterios establecidos para decretar una persona como recuperada[8]. Ambas situaciones generan dificultades para obtener una proyección epidemiológica con mayor certeza.
Otro elemento relevante es la falta de estudios nacionales de proyección de COVID-19 mediante el uso del modelo Susceptible-Expuesto-Infectado-Recuperado en Chile. Nuevas investigaciones permitirán comparar resultados, e ir generando conocimiento acumulado para favorecer las acciones de salud pública a nivel nacional, regional y comunal.
Conclusiones
Esta investigación tuvo como objetivo estimar la trayectoria epidemiológica del Covid-19, considerando tres escenarios posibles en función de la definición nacional y de las organizaciones internacionales en salud respecto al estado de “recuperado”. Asimismo, supone ser un aporte en la comprensión del comportamiento de la enfermedad con el fin de disminuir el impacto negativo del virus en Chile.
Se ajustó un modelo Susceptible-Expuesto-Infectado-Recuperado generalizado para conocer la dinámica del brote y sus características. A diferencia del modelo clásico, el modelo ajustado incorpora el estado de cuarentena y recuperado que, juntos, reemplazan el estado recuperado original en el modelo Susceptible, Infectado y Recuperado. En consecuencia, se explican los casos infectados confirmados, los recuperados y los fallecimientos informados. Analizando los datos oficiales del Ministerio de Salud, se estimaron los parámetros para COVID-19 como el tiempo latente, el tiempo de cuarentena y el número de reproducción básico.
Por todo lo anterior, el análisis expuesto no pretende ser una estimación exacta de la proyección del COVID-19 en Chile. Por el contrario, los hallazgos están asociados a las diferencias encontradas en la comparación de escenarios. En esta línea, la presente investigación evidenció que el concepto de recuperación de COVID-19 puede resultar decisivo para la estimación de la magnitud de pandemia en el país.
A modo de sugerencia, se insta a las autoridades a generar reportes considerando las recomendaciones de las organizaciones internacionales de salud (Organización Mundial de la Salud, Centro de Control y prevención de enfermedades, Centro Europeo para la Prevención y Control de Enfermedades) en cuanto a declarar a las personas como recuperadas de COVID-19, como también en no adicionar a los fallecidos en la lista de recuperados, ya que ambos estados son diferentes. La utilización de los datos del Ministerio de Salud con el actual criterio de recuperados puede llevar a subestimar la proyección de COVID-19 en Chile y generar nuevos máximos de la enfermedad en meses posteriores.
Asimismo, emplazamos a las autoridades a aumentar las pruebas de laboratorio para la confirmación de COVID-19 y evitar demoras en los resultados. Esto implicará el llevar a cabo cuarentenas a las personas afectadas de COVID-19 y evitar la diseminación. En esa misma dirección, a propósito de las estimaciones de los escenarios 2 y 3, se sugiere continuar con las medidas preventivas al menos hasta septiembre del presente año.
Para finalizar, a modo de reflexión queremos mencionar que los modelos matemáticos/epidemiológicos son limitados en el entendimiento global de los eventos epidémicos, pues sus aproximaciones se realizan bajo un paradigma netamente cuantitativo y las consecuencias del COVID-19 son multidimensionales. En ese sentido, este aporte analítico puede ser provechoso toda vez que se incluyan en otras investigaciones, discusiones o aproximaciones, elementos socio-estructurales y de determinación social. Resulta imperativo incluir estos elementos en el análisis global del COVID-19 debido al análisis cuantitativo hegemónico, observado en este evento.
Por ello, nos llama la atención el escaso esfuerzo institucional para asegurar la participación de quienes, desde el ámbito social, son parte importante de las posibles resoluciones de esta situación sanitaria. Voces de trabajadores/as, organizaciones de salud, organizaciones sociales y territoriales, universidades, centros de investigación, entre otras, pueden ser tremendamente provechosas para este contexto. Por lo tanto, conminamos a ampliar el debate en pos de enfrentar esta crisis sanitaria desde una perspectiva multidimensional.

