Introducción

El primer caso de infección por SARS-CoV-2 fue reportado en China continental el 31 de diciembre 2019[1], luego de un brote de síndrome respiratorio agudo severo por coronavirus 2 (SARS-CoV-2) atribuido a COVID-19, alcanzando una dimensión global en sólo cuatro semanas[2]. La Organización Mundial de la Salud (OMS) declaró el estado de pandemia el 30 de enero de 2020[1] y recomendó un conjunto de estrategias de mitigación para frenar el contagio. Entre estas destacan la adopción de medidas de distanciamiento social, aplicación de pruebas diagnósticas y confinamiento de casos[1].

En Chile, se han adoptado medidas de distanciamiento social orientadas a reducir el riesgo de infección, entregando tiempo al sistema de salud para aumentar los recursos disponibles para pacientes críticos. Entre estas se cuentan el cierre de colegios, la limitación de actividades comerciales, el cierre de fronteras, la instalación de cordones sanitarios e imposición de limitaciones al desplazamiento[3], junto a otras como aumento del tamizaje diagnóstico[4]. Sin embargo, la propagación de COVID-19 continúa y al 5 de mayo de 2020 se ha llegado a más de 22 000 casos confirmados, con una tasa de letalidad de 1,3%[5]. Córdova y colaboradores[6] desarrollaron un modelo matemático que estima que unas 100 000 personas estarían infectadas por COVID-19 en Chile a fines del mes de junio. En tanto, información de diferentes países muestran que alrededor del 15% de los pacientes infectados necesitarán hospitalización y de estos, un tercio (5% del total) requerirá de cuidados intensivos[7].

Uno de los países más afectados ha sido Italia, donde en la región de Lombardía la demanda de camas de unidad de cuidados intensivos por pacientes COVID-19 previa a la crisis era de 2,9%, mientras que al 15 de marzo alcanzó la alarmante cifra de 16%[7]. Estas unidades de cuidados intensivos suelen tener una ocupación que varía según países entre el 75 y el 90%. De acuerdo con los datos disponibles a nivel nacional, entre el 5 de abril y el 5 de mayo, 4,1% de los pacientes confirmados en Chile ha requerido hospitalización en unidades de cuidado intensivo[5].

En Chile, de acuerdo con información obtenida desde la Unidad de Gestión de Camas Críticas del Ministerio de Salud, al momento de la redacción de este trabajo, aproximadamente un 80% de ellas se encuentran ocupadas por pacientes con otras dolencias[8]. Por esta razón, sumado a las proyecciones de casos COVID-19 y la subsecuente demanda de ingresos hospitalarios en unidades de cuidados críticos, es factible suponer que la saturación de la oferta de camas críticas no es cuestión de si ocurrirá, sino cuándo ocurrirá. En una encuesta realizada en 175 hospitales australianos entre el 13 y el 24 de marzo, se determinó que el número original de camas críticas fue triplicado[9] como respuesta a la incidencia de casos. Entre el 5 de abril y el 5 de mayo, Australia reportó una letalidad promedio de 1,1%[5]. Urge, por tanto, la necesidad de contar no sólo con un sistema de gestión diaria del número de camas críticas (Unidad de Gestión de Camas Críticas del - Ministerio de Salud), sino con una proyección de la necesidad de estas durante el desarrollo de la pandemia para anteponerse al escenario adverso de saturación y gestionar a priori la adquisición/reconversión/habilitación de nuevas unidades, ya sea a nivel local, regional o nacional.

El objetivo de este trabajo es proponer un modelo predictivo para estimar la demanda esperada de pacientes COVID-19 que requerirán hospitalización en unidades hospitalarias de cuidados críticos, basado en la estimación previa del número de personas que podrían adquirir y desarrollar COVID-19. Además, se busca elaborar un índice de saturación, que describa la relación entre el número de pacientes COVID-19 que requerirán de cuidados críticos y la oferta de camas críticas, sobre la base de la función de Gompertz. Esta, corresponde a una función de tipo no lineal que se adapta adecuadamente para describir procesos biológicos. Es frecuentemente utilizada en cinética bacteriana y de crecimiento tumoral[10],[11].

Para el modelamiento se utilizó el número de casos COVID-19 diarios confirmados y reportados entre el 4 de marzo y el 5 de mayo de 2020. A continuación, se construyó un índice de saturación que describe la relación entre el número de pacientes COVID-19 que requerirán de cuidados críticos y la oferta de camas críticas. En el modelo se incluyen variables relativamente sencillas de obtener desde fuentes de acceso público, tales como incidencia diaria de casos COVID-19, número de pacientes hospitalizados por dicha patología en unidades críticas, índice ocupacional de camas críticas y oferta de camas críticas disponibles. Así, el modelo puede ser aplicado hoy, tanto a nivel nacional como en multiniveles para estimar la evolución de la demanda de camas críticas por pacientes COVID-19 en las próximas semanas. Esto quiere decir que el modelo puede replicarse en regiones, municipios, servicios de salud y hospitales.

Metodología

Fuentes de información

Se analizó un total de 22 016 pacientes con diagnóstico confirmado para COVID-19 ocurridos en Chile, entre el 4 de marzo y el 5 de mayo de 2020, obtenidos a partir de los reportes oficiales emitidos diariamente por el Ministerio de Salud de Chile, validados en el sitio web oficial de la OMS y publicados en tiempo real en el sitio WORLDOMETER[5].

A partir de la información sobre dotación de camas críticas publicadas por el Ministerio de Salud[12], así como de información emitida recientemente en medios de prensa por el ministro de salud[13] y por el Colegio Médico de Chile[14], se estimó el número actual de camas críticas totales disponibles a nivel nacional entre 1900 y 2200 unidades. Dado que un porcentaje de la dotación de camas hospitalarias se encuentra ocupado por pacientes con otras dolencias en un momento dado, se aplica como factor de corrección el índice ocupacional o número de camas ocupadas dividido por el número total de camas disponibles a un tiempo dado. Este indicador es publicado periódicamente por el Ministerio de Salud[8] y su valor actual varía entre 0,75 y 0,85. La literatura actual concuerda que aproximadamente el 5% de los pacientes COVID-19 requerirá hospitalización en unidades de cuidados intensivos. De acuerdo con los datos observados, en Chile este porcentaje ha alcanzado un 4,1% entre el 15 de marzo y el 5 de mayo.

Modelamiento

Para estimar el número de personas que podrían infectarse y desarrollar COVID-19 dentro de las próximas semanas, se utilizó la función de Gompertz. Esta corresponde a una curva con crecimiento inicial de tipo exponencial, seguida de un crecimiento logarítmico (curva sigmoidea) que, a diferencia de la función logística general, presenta un crecimiento inicial menos acentuado. Dicho crecimiento inicial se correlaciona mejor con la dinámica de aparición de contagios por COVID-19 observada hasta ahora en nuestro país. La función de Gompertz consta de tres parámetros que pueden ser ajustados a un set de datos dados. Una vez obtenido un número suficiente de valores proyectados por el modelo, ambas series (valores observados y datos modelados) fueron sometidas a la prueba de ANOVA para determinar robustez del modelo. La Figura 1 muestra la función de Gompertz, la expresión utilizada para este estudio y los parámetros utilizados por el modelo:

Figura 1.

Función de Gompertz.

Preparada por los autores a partir de los resultados del estudio.

Tamaño completo

Una vez obtenido los parámetros y el modelo ajustado, a un tiempo t, se obtuvo el modelo que estima los casos COVID-19 esperados. En este caso, el modelo se aplica a un total de 134 días (4 de marzo al 15 de julio de 2020). Para el modelamiento y cálculos se utilizó el software estadístico SPSS versión 20, mientras que para las gráficas se utilizó el software Microsoft Excel 2019.

Índice de saturación

Para establecer el punto en el cual la demanda de camas críticas por pacientes COVID-19 alcanzará el 100% de la oferta disponible, se utilizará un modelo descrito previamente por González y colaboradores[15], quienes realizaron similar análisis a partir de datos de pacientes COVID-19 disponibles hasta el 23 de marzo. En nuestro estudio, utilizamos similar método pero se ajustaron las variables índice ocupacional, camas críticas totales y camas de cuidados intensivos para pacientes COVID-19, para obtener distintos escenarios. Adicionalmente, se asumirá una liberación de camas de cuidados intensivos para pacientes COVID-19 cada 10 días. La función desarrollada es la siguiente (Figura 2):

Figura 2.

Función para el cálculo del índice de saturación.

Preparada por los autores a partir de los resultados del estudio.

Tamaño completo

Resultados

A partir del número oficial de casos COVID-19 confirmados acumulados entre el 4 de marzo y el 5 de mayo, se obtuvo un modelo de casos esperados basado en la función de Gompertz, de tipo logístico, con ajuste según prueba ANOVA de 99% (r = 0,998), cuyo resumen puede observarse en la Tabla 1. 

Tabla 1.

Modelo de Gompertz a partir de registros de casos COVID-19 acumulados del 4 de marzo al 5 de mayo de 2020.

Preparada por los autores a partir de los resultados del estudio.

Tamaño completo

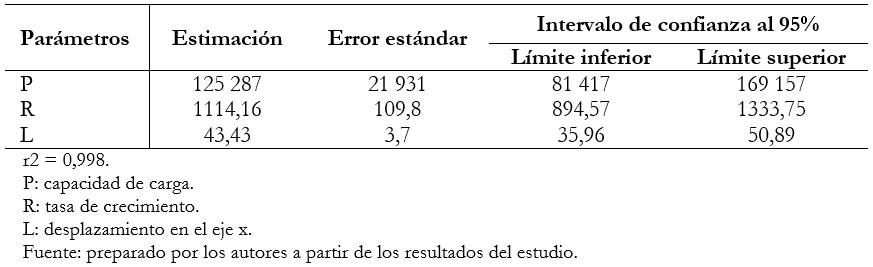
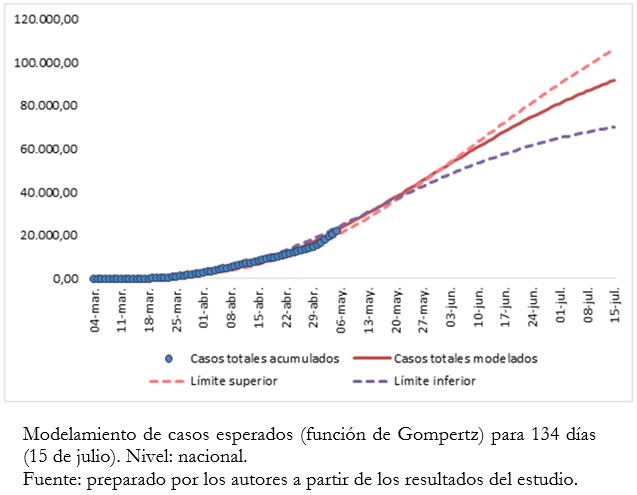
La gráfica del modelo anterior, utilizando los parámetros obtenidos (P, R y L) y los intervalos de confianza (límite inferior y límite superior), da como resultado una curva de tipo sigmoidea, con un aumento exponencial de casos en las fases iniciales y con un aplanamiento progresivo de la curva, la que puede ser observada en la Figura 3. Mediante el modelo obtenido y los datos observados que han sido incorporados en la misma figura, se puede estimar que a fines del periodo analizado (día 134, que correspondería a mediados del mes de julio), poco más de 92 000 personas podrían figurar en el registro oficial de contagios por COVID-19 a nivel nacional. Esta estimación presenta un rango de dispersión importante (diferencia entre los límites de confianza), en parte debido al fuerte incremento de registro de casos observado en los últimos días analizados, pasando de 17 000 a 22 000 casos totales en sólo cuatro días.

Figura 3.

Casos COVID-19 observados y registrados entre el 4 de marzo y el 5 de mayo de 2020.

Preparada por los autores a partir de los resultados del estudio.

Tamaño completo

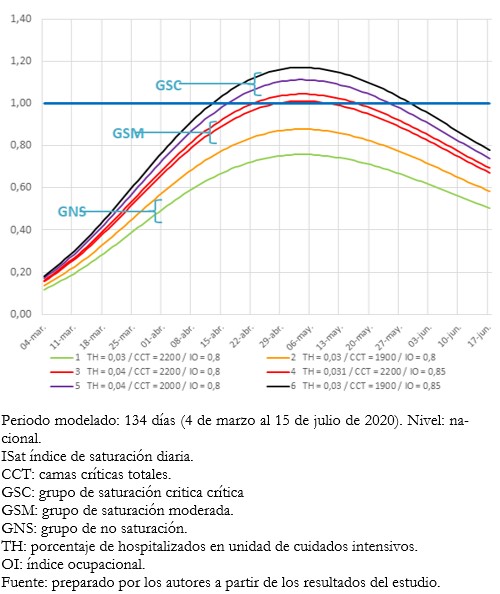
La Figura 4, por su parte, muestra la evolución del índice de saturación en un intervalo de 106 días. Esto corresponde al período entre el 1 de abril y el 15 de julio del presente año, para 6 escenarios distintos y estimado a partir del modelamiento de contagios entre el 4 de marzo y el 15 de julio del presente año. Siendo el escenario N° 1 el más favorable (curva más cercana al eje horizontal), y el escenario N° 6 el más desfavorable. El escenario N° 1, (curva en verde claro) asume una dotación de 2200 camas críticas totales disponibles a nivel nacional para todo paciente que lo requiera (no exclusivamente pacientes COVID-19), con un índice ocupacional de 0,80 u 80% de ocupación inicial, lo que se traduce en un 20% de disponibilidad real, esto es, unas 440 camas. En este mismo caso, se asume además que un 3% de pacientes COVID-19 confirmados como positivos requerirán uso de una cama crítica. Finalmente, para éste y todos los escenarios restantes, se estima un tiempo de hospitalización medio en unidades de cuidados intensivos (uso medio de cama crítica) de 10 días.

En este primer escenario, el índice de saturación máximo obtenido es de 0,75; por lo que representa el escenario más favorable (más lejano al punto de saturación). El escenario N° 2 (línea color naranja) es similar al anterior, pero asume una dotación de 1900 camas críticas totales (380 camas disponibles efectivas). En este caso, el índice de saturación máximo alcanzado es aproximadamente 0,88. A estos dos escenarios los denominamos grupo de no saturación o GNS.

El escenario N° 3 asume similares condiciones del escenario N° 1 pero aumentando la tasa de hospitalización a 4,0% y la demanda de camas críticas para pacientes COVID-19 a 2200 unidades. En estas condiciones, el índice de saturación máximo alcanzado es de 1,01; lo que implica que el punto de saturación es sobrepasado. El período de saturación se extiende entre el 26 de mayo y el 10 de junio, totalizando 15 días. El escenario N° 4 contempla una dotación total de camas críticas de 2200 unidades, una tasa de hospitalización de 3,1% y un índice ocupacional de 0,85. Este último valor se traduce en un total de 330 camas disponibles efectivas. En este escenario, el índice de saturación máximo alcanza a 1,04; lo que implica que el punto de saturación es también sobrepasado entre el 20 de mayo y el 15 de junio (27 días). Los escenarios 3 y 4 corresponden al grupo de saturación moderada o GSM.

En el escenario N° 5, con una dotación de 2000 camas críticas totales, un índice ocupacional de 0,80 (400 camas disponibles efectivas) y 4,0% de demanda de hospitalización (camas de cuidados intensivos para pacientes COVID-19 igual a 4,0%) se alcanza un índice de saturación máximo de 1,11. En este escenario, el punto de saturación es sobrepasado entre el 14 de mayo y el 23 de junio (41 días). Finalmente, los parámetros asumidos para el escenario N° 6 son 1900 camas críticas totales, un índice ocupacional de 0,85 y una demanda por pacientes COVID-19 esperada de 3,0%. En este escenario, el índice de saturación máximo llega a 1,17 y la saturación se extiende entre el 10 de mayo y el 27 de junio (49 días). Los dos últimos escenarios corresponden al denominado grupo de saturación crítica o GSC. 

Figura 4.

Índice de saturación diaria de camas críticas totales asociado a demanda por pacientes COVID-19 en 6 escenarios.

Preparada por los autores a partir de los resultados del estudio.

Tamaño completo

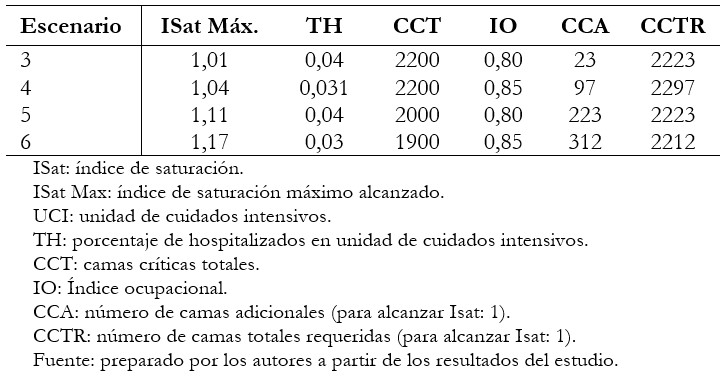
Los resultados expuestos permiten obtener a partir de los índices de saturación diarios, el número aproximados de camas de cuidados críticos adicionales que serán requeridas por las unidades de cuidados críticos en aquellos escenarios propuestos, en que el punto de saturación (índice de saturación es igual a 100%) es sobrepasado. La Tabla 2 muestra los escenarios en que se sobrepasa el índice de saturación de 100%; y para cada caso, indica los índices de saturación máximos alcanzados, los parámetros utilizados, el número de camas críticas adicionales que serán requeridas y el número de camas críticas totales requeridas. De esta tabla se puede inferir que en todos los escenarios de saturación expuestos, sería esencial para controlar la saturación un aumento en la dotación de camas críticas totales de al menos 2300 unidades totales. Sin embargo, es importante señalar que tanto el número de camas críticas adicionales como el número de camas críticas totales, corresponden a las unidades necesarias sólo para volver al estado de saturación exacta, es decir, índice de saturación de 100%. Resulta evidente entonces que, para lograr un margen de seguridad adecuado, en la práctica el número de camas adicionales debiese ser mayor y corresponderse con un índice de saturación de 0,5 o inferior.

Tabla 2.

Escenarios en que se supera oferta de camas UCI disponibles (ISat > 1) y N° de camas adicionales para compensación (volver a ISat =1).

Preparada por los autores a partir de los resultados del estudio.

Tamaño completo

Discusión

Considerando la situación de los servicios hospitalarios frente a la pandemia generada por la emergencia del COVID-19, el presente trabajo tuvo como propósito ofrecer una alternativa simple para estimar el momento de saturación de las camas de cuidados críticos (camas críticas) disponibles a nivel nacional y que a la vez, permita estimar el número de unidades que serán requeridas para compensar esta saturación. Dado que el índice de saturación representa en esencia una relación entre la demanda esperada de camas críticas y la oferta disponible, el área bajo la curva del índice de saturación en los diferentes escenarios, a partir del valor de saturación (índice de saturación igual a 1) representa el número estimado de camas críticas que serán requeridas para compensar escenarios de saturación.

El modelamiento de la demanda de camas críticas utilizando la función de Gompertz, muestra resultados robustos en relación con la dinámica de contagio hasta ahora observada, debido al brote epidémico de COVID-19 durante la etapa de crecimiento exponencial en la que actualmente nos encontramos. Las estimaciones del número final de casos pueden mostrar variabilidad significativa ya que dependen en gran medida de las acciones de control y/o mitigación de la epidemia que las autoridades implementen, las que no son parte del alcance de este trabajo.

Al analizar los escenarios descritos de manera conjunta se puede observar que el índice de saturación es altamente sensible a cambios en las tres variables asociadas a la dinámica de utilización de camas críticas. Esto es, la capacidad instalada de camas críticas totales, el índice ocupacional de dichas camas y la demanda esperada de pacientes COVID-19 que requerirán de hospitalización en unidades de cuidados críticos. Particular atención merece el índice ocupacional, cuyo valor ha sido estimado entre 0,75 y 0,85; siendo altamente probable que durante el período invernal (de junio a agosto) predominen valores más cercanos a 0,85 o incluso superiores.

Es importante reiterar que, a partir del momento de saturación de camas críticas, todo paciente que requiera utilizar una de estas unidades se encuentra en serio riesgo de muerte. Más aún, los registros de pacientes hospitalizados en unidades críticas por COVID-19 disponibles muestran que hasta ahora, aproximadamente el 82% de estos pacientes ha requerido de ventilación mecánica, lo que se traduce en un significativo riesgo de muerte para pacientes COVID-19 con incapacidad de acceder a una cama crítica. Una proyección de demanda de camas en unidades de cuidados intensivos (críticas) realizada por M. Canals[16], basada en el número de reproducción (R0) de la curva de contagios, estimó para diferentes escenarios (R0 distintos) un margen de saturación de camas críticas entre la semana del 20 al 26 de abril y la semana entre el 10 y 18 de mayo, siendo este último escenario consistente con los resultados de este trabajo.

Pero la situación actual, desafortunadamente, podría ser menos promisoria. Al 6 de mayo, el país tuvo seis días consecutivos con un promedio de casi 1200 casos COVID-19 nuevos por día (10% de ellos asintomáticos), casi tres veces lo observado durante todo el mes de abril (422 casos por día). Este hecho es preocupante ya que de mantenerse este ritmo de incidencia de casos (1200 por día), al día 85 (27 de mayo) podrían haber más de 50 000 casos confirmados sintomáticos y hasta cinco de los seis escenarios analizados en este trabajo podrían eventualmente alcanzar un índice de saturación igual a 1.

Adicionalmente, es importante mencionar que en ninguno de los casos analizados en este trabajo, se ha incorporado el efecto en la demanda y en la letalidad una vez alcanzados los índices de saturación. El hecho de no disponer da camas críticas en forma oportuna para pacientes que lo requieran implica por una parte que, tanto pacientes COVID-19 como no COVID-19 en condiciones más severas, ven fuertemente reducidas sus posibilidades de sobrevivir. Sumado a ello, la falta de recursos humanos e insumos, la redistribución de recursos y el efecto de “cuello de botella”, podrían resultar en un agravamiento de pacientes en condición menos grave, que podrían pasar a requerir de cuidados críticos, agregando aún más presión sobre el sistema.

Este estudio ha sido realizado a escala nacional, pero su principal fortaleza es que ha sido pensado en la lógica de aportar con un modelo de estimación de demanda de camas críticas simple, fácil de interpretar y sencillo de implementar a cualquier nivel de necesidad ya sea en un hospital, en un Servicio de Salud, en municipios u otros. Hoy, la información necesaria para realizar este modelamiento se encuentra disponible en diversas fuentes públicas e intrahospitalarias, por lo que su uso puede ser de ayuda en la gestión de demanda de camas críticas a todo nivel en el contexto de la pandemia por COVID-19.

Limitaciones del estudio

Para este estudio se utilizaron los registros de pacientes COVID-19 confirmados y publicados al 5 de mayo en fuentes oficiales. Por lo tanto, los resultados y conclusiones de este dependen de la precisión y consistencia de dichos registros. Además, el modelamiento de datos realizado no incorpora variables asociadas a intervenciones tales como cuarentenas parciales, medias de distanciamiento social, exámenes masivos de diagnóstico COVID-19 y otras implementadas por el gobierno, que pudieran cambiar significativamente la incidencia de casos durante el periodo estudiado. Tampoco se consideraron para este modelamiento variaciones específicas del comportamiento de la cinética de contagios por COVID-19, tales como el número de reproducción (R0) o el tiempo de duplicación de casos; parámetros cuya variación en el tiempo podrían afectar las proyecciones aquí realizadas. Por último, las proyecciones presentadas se extienden hasta el 15 de julio de 2020. Estas pueden ser significativamente influidas por la dinámica de aparición de enfermedades estacionales invernales, lo que no han sido explícitamente incluidas en este estudio.

Conclusión

A la luz de los resultados obtenidos, se puede establecer una ventana de operaciones relativamente estrecha, de 4 a 8 semanas, para mitigar la inminente saturación de camas críticas hospitalarias producto de la demanda de pacientes COVID-19.

Esta estimación se basa principalmente en un aumento de, al menos, 2300 camas críticas totales, en la posibilidad de reducir la tasa de hospitalización en unidad de cuidados intensivos a 3% o inferior, y de mantener un índice ocupacional no superior a 0,85.

Notas

Roles de autoría

Financiamiento

Conflictos de intereses

Comité de ética Institucional

Autoría de figuras