Análisis
← vista completaPublicado el 13 de febrero de 2021 | http://doi.org/10.5867/medwave.2021.01.8119
COVID-19 en Chile: la utilidad de los modelos epidémicos simples en la práctica
COVID-19 in Chile: The usefulness of simple epidemic models in practice
Resumen
Objetivos El objetivo general ha sido describir y evaluar el valor predictivo de tres modelos durante el desarrollo de la epidemia COVID-19 en Chile, aportando conocimiento para la toma de decisiones en salud.
Métodos Desarrollamos tres modelos a lo largo de la epidemia: un modelo discreto para predecir a corto tiempo la máxima carga sobre el sistema de salud, un modelo básico SEIR (susceptibles-expuestos-infectados-removidos) con ecuaciones discretas; un modelo SEIR estocástico con método de Montecarlo; y un modelo de tipo Gompertz para la Región Metropolitana (Santiago).
Resultados El modelo de máxima carga potencial ha sido útil durante todo el seguimiento de la epidemia proporcionando una cota superior para el número de casos, la ocupación de unidades de cuidados intensivos y el número de fallecidos. Los modelos SEIR determinístico y estocástico tuvieron gran utilidad en la predicción del ascenso de los casos, el máximo y el inicio del descenso de casos, perdiendo utilidad en la situación actual por el reclutamiento asincrónico de casos en las regiones y la persistencia de una endemia alta. El modelo de Gompertz ha tenido un mejor ajuste en el descenso ya que esta captura mejor la asimetría de la curva epidémica en Santiago.
Conclusiones Los modelos han demostrado gran utilidad en el seguimiento de la epidemia en Chile, con distintos objetivos en distintas etapas de la epidemia. Han complementado los indicadores empíricos como casos reportados, letalidad, fallecimientos y otros, permitiendo predecir situaciones de interés y visualizar la conducta a corto y largo plazo de esta pandemia a nivel local.
Ideas clave
- Los modelos matemáticos juegan un papel importante en el seguimiento de las epidemias, ayudando a racionalizar la toma de decisiones y a predecir eventos importantes en el curso de las mismas como aumento, máximo y disminución de la incidencia.
- Los modelos más simples pueden ser un gran aporte para el monitoreo y predicción de epidemias, para comprender y monitorear la dinámica de la pandemia COVID-19 y contribuir a la toma de decisiones.
- Estudiamos la capacidad predictiva de tres modelos matemáticos simples durante la epidemia COVID 19 en Chile.
- En este reporte informamos y discutimos la utilidad, los aciertos y las dificultades prácticas que hemos tenido en su desarrollo.
Introducción
Desde que Daniel Bernoulli utilizó un método matemático en 1766 para evaluar la efectividad de la variolación hasta la actualidad, se han desarrollado una gran cantidad de modelos y conceptos matemático-epidemiológicos para estudiar y seguir el comportamiento de diferentes enfermedades infecciosas en la población. Numerosos autores como J. Brownlee (1906, 1918), R. Ross (1911, 1917), McKendrick y Kermack (1927), Reed y Frost (1928) entre otros, contribuyeron al desarrollo de esta área del conocimiento[1]. Posteriormente, hubo un gran desarrollo que incluyó la dimensión espacial, la estacionalidad y el papel de los portadores, la transmisión venérea y otros. Entre ellos, destacan los aportes de Anderson y May (1978), de Hudson y Dobson a partir de 1985 y de Roberts y Grenfell en la década de los 90[1]. Un gran número de estudios destacaron conceptos como población umbral, inmunidad colectiva[2],[3],[4],[5], número reproductivo, intervalo serial, tiempos de incubación y derrame en la dinámica de las enfermedades infecciosas. Todos estos conceptos contribuyen de alguna manera a la toma de decisiones[6],[7],[8]. En las últimas décadas se ha hecho hincapié en la propagación espacial[9],[10],[11],[12],[13],[14],[15],[16],[17], el papel de la población la movilidad y la conectividad de las redes de transporte, como las aerolíneas, en la propagación de epidemias[18],[19],[20],[21],[22],[23]. Estos modelos han hecho grandes contribuciones al estudio de diferentes enfermedades como Influenza AH1N1, AH5N1, VIH, SARS y Ébola[18],[19],[20],[21],[22].
Se han desarrollado numerosos modelos para la actual epidemia de COVID-19, una enfermedad causada por el virus SARS-CoV-2, y para el SARS[24],[25],[26],[27]. La mayoría corresponden a modelos SEIR con diferentes tipos de estratificación, ya sea espacial, por edad, socioeconómica, entre otros. Dada la gran complejidad de las formas de propagación, los modelos matemáticos pueden ofrecer herramientas valiosas para sintetizar información comprender los patrones epidemiológicos y desarrollar evidencia cuantitativa para informar la toma de decisiones en salud global[6].
En Chile, se ha utilizado con éxito un modelo para pronosticar la ocupación de unidades de cuidados intensivos a corto plazo, advirtiendo a las autoridades del posible colapso de la capacidad hospitalaria[28] y modelos tipo SEIR para predecir la evolución de la epidemia localmente[29]. Otro estudio utiliza un modelo de ajuste cúbico polinomial para estimar el número de casos y un modelo exponencial para representar el esfuerzo diario para reducir la tasa de crecimiento diaria inicial para advertir del potencial de la pandemia[30]. Además, otro estudio analizó el esfuerzo diario mínimo para que el sistema de salud no colapse durante el brote de COVID-19. Se obtiene así una condición de umbral paramétrico, que involucra un parámetro asociado al mínimo esfuerzo diario para no colapsar el sistema[31]. Todos han contribuido a destacar la importancia de la modelación en la toma de decisiones[32].
La pandemia COVID-19 ha costado más de 12 mil muertes en Chile. Inicialmente tuvo un crecimiento acelerado que fue parcialmente controlado con intervenciones como el cierre de escuelas y universidades, y cuarentenas parciales. Luego de las medidas iniciales, hubo una relajación de intervenciones e intervenciones tardías que derivaron en una gran epidemia concentrada principalmente en la Región Metropolitana (Santiago), a pesar de las advertencias realizadas por la comunidad científica y diferentes equipos de modelado de epidemias. Posteriormente, se establecieron cuarentenas masivas que se han asociado a una disminución en el número de casos y que han llevado a un número relativamente estable de entre mil y dos mil casos diarios en el país[33]. A lo largo de este proceso, una serie de factores han complicado el seguimiento de los casos, como cambios en el sistema de notificación y subregistro de casos.
Considerando que los modelos más simples pueden ser un gran aporte para el monitoreo y predicción de epidemias, hemos desarrollado tres enfoques matemáticos simples para comprender y monitorear la dinámica de la pandemia COVID-19 y, con ello, contribuir a la toma de decisiones en Chile. En este aporte informamos y discutimos la utilidad, los aciertos y las dificultades prácticas que hemos tenido en su desarrollo.
Métodos
Realizamos un estudio ecológico utilizando reportes públicos diarios oficiales del Ministerio de Salud de Chile incluyendo nuevos casos confirmados, casos que requirieron ingreso a la unidad de cuidados intensivos y muertes atribuibles a COVID-19 a nivel nacional y subnacional (regiones). Con esta información hicimos:
- Estimaciones del número reproductivo efectivo Rt.
- Estimaciones del subregistro de casos.
- Desarrollamos tres modelos con diferentes objetivos para seguir la epidemia en Chile.
Calculamos Rt utilizando el método desarrollado por Cori y colaboradores[34]. Consideramos las últimas 2 semanas (14 días) y un intervalo serial τ = 5 días con variabilidad entre 2 y 8 días (basado en[35],[36],[37]). El subregistro de casos se estimó según el método propuesto por Russell y colaboradores[38],[39] adaptado a la situación chilena[33].
Modelo de carga potencial máxima
El objetivo de este modelo ha sido seguir la evolución de la curva epidémica y establecer predicciones a corto plazo (1 semana) de las cargas potenciales máximas de nuevos casos, ocupación de unidades de cuidados intensivos y defunciones. Con ello se busca estimar el nivel de saturación del sistema de salud, lo que permitiría informar decisiones que apuntan a reducir el número de infecciones o aumentar la capacidad de respuesta del sistema de salud.
Si hay casos nuevos de Ct en una semana “t” y hay It personas infectadas con It = (Ct + Ct-1), considerando que los casos permanecen contagiosos hasta por dos semanas, se puede proponer que:
Ct+1 ≈ Rt (Ct + Ct-1).
Esto significa que todos los infectados en las dos semanas anteriores son contagiosos y contribuirán a las infecciones la semana siguiente. Sin embargo, no todas las personas infectadas en un día "i" contribuyen con casos a la semana siguiente. Esto depende del intervalo serial y su distribución de probabilidad. Una expresión más adecuada es:
![]() , t en semanas, i en días, donde tf representa el último día de la semana “t”, pi representa la probabilidad de que alguien infectado el día "tf-i" infecte a alguien en la semana t + 1. Por lo tanto, una mejor expresión es:
, t en semanas, i en días, donde tf representa el último día de la semana “t”, pi representa la probabilidad de que alguien infectado el día "tf-i" infecte a alguien en la semana t + 1. Por lo tanto, una mejor expresión es:
Ct+1 ≈ fRt (Ct + Ct-1) (1).
Donde f corresponde a un factor de corrección como consecuencia de la distribución de probabilidad del intervalo serial. Para una carga máxima, el factor de corrección se estima como el máximo pi (i = 0 a 13) para una distribución γ con una media de 5 y una desviación estándar de 4,3 días (basado en[35],[36],[37]); el factor de corrección es f ≈0,8. La ecuación (2) es similar a una serie de Fibonacci y requiere dos condiciones iniciales (t1 y t2). En este estudio, estos fueron t1 = 10 (8 de marzo), t2 = 65 (15 de marzo) (los casos nuevos en las dos primeras semanas).
Considerando que aproximadamente el 3,5% de los casos llegan a unidades de cuidados intensivos (0,035Ct); que en promedio una de estas dependencias está ocupada durante aproximadamente dos semanas, y que la latencia entre el inicio de los síntomas y el requerimiento de la unidad de cuidados intensivos es de aproximadamente 1 semana[38],[39], se puede proponer que las unidades de cuidados intensivos ocupadas (Ut):
Ut+1 = 0,035 (Ct + Ct-1) (2).
Para estimar el número máximo de muertes (Dt) consideramos una latencia de dos semanas entre el inicio de los síntomas y una letalidad de los pacientes sintomáticos del 2,6%[38],[39]. Entonces: Dt+1 = 0.026Tt-1 (3) donde Tt-1 corresponde al número total de casos de hace dos semanas. Por lo tanto, las ecuaciones (1), (2) y (3) constituyen la base de este modelo.
Este modelo permite predecir la carga potencial máxima de COVID-19 esperada para la semana siguiente, basándose en el “historial” de las dos semanas anteriores.
Modelo SEIR discreto y modelo estocástico
El objetivo de este modelo ha sido intentar predecir la forma de la curva epidémica y los tiempos en los que se produciría el aumento del número de casos, el máximo de casos y la disminución de la forma más precoz posible. Usamos una variación de un modelo SEIR: Susceptible (S), Latente (E), Infeccioso (I), removido (fallecido + recuperado (Rm), en su forma discreta:
Si+1 = Si – βSiIi (4).
Ei+1 = Ei + βSiIi – νEi (5).
I i+1 = I i + νEi – (μ + γ) Ii (6).
Rmi+1 = Rmi + (μ + γ) Ii (7).
Ci+1 = pIi (8).
Ui+1 = qCi-7 (9).
Di+1 = hTi-14 (10).
Donde β es el coeficiente de transmisión, ν la tasa de transferencia de E a I, µ la tasa de mortalidad, γ la tasa de recuperación, p la proporción de infectados que son notificados, q la proporción de pacientes sintomáticos que requieren unidad de cuidados intensivos y h la tasa de mortalidad. El subíndice "i" representa el tiempo en días. En este estudio se consideraron constantes los parámetros ν = 1/5 días-1, (µ + γ) = 1/14 días-1, p = 0,1, q= 0,035 y h = 0,026 y el coeficiente de transmisión β y la asíntota del modelo "S*" como parámetros variables.
El modelo se ajustó a medida que avanzaba la epidemia, dependiendo de los cambios ocurridos en el número de reportados y en el sistema de notificación. Inicialmente al 15 de abril, la asíntota del modelo "S*" se estimó considerando una población chilena de 19 000 000, una proporción de inmunidad colectiva del 57,4%, que el 5% podría enfermarse (según la experiencia europea) y un factor de corrección de heterogeneidad de 0,5 considerando que en este momento la epidemia se centró en Santiago. Por lo tanto, S* inicial = 19 000 000 x 0,547 x 0,5 x 0,05 = 259 825 casos. El coeficiente de transmisión β se estimó ajustando el mejor modelo. El modelo se ajustó semanalmente (si fue necesario) variando S* y β. La bondad de ajuste del modelo se estudió con el coeficiente de determinación (R2) y su significación estadística (prueba F).
Dada la gran variabilidad y fluctuaciones estocásticas de los casos a nivel mundial, para incluir sus efectos sobre la dinámica se consideró la versión estocástica simple del modelo anterior, con los mismos parámetros, basados en las ecuaciones (4) a (7), con el método cinético de Monte Carlo incorporando el algoritmo de Gillespie[40]. En esto, consideramos los tres eventos:
Un latente ocurre con tasa a1: βS(i)I(i); S = S-1; E = E+1;
Un infectado ocurre con tasa a2: νE(i); E =E-1; I = I+1
Un removido ocurre con tasa a3: (μ + γ)I(i); I =I-1; Rm =Rm+1
La probabilidad para aj es:![]() . El tiempo hasta el siguiente evento (τ) se distribuye exponencialmente, con una tasa igual a la suma de las tasas de todos los eventos posibles: f(τ) = ∑ jα je-τ∑ jaj, con un valor esperado
. El tiempo hasta el siguiente evento (τ) se distribuye exponencialmente, con una tasa igual a la suma de las tasas de todos los eventos posibles: f(τ) = ∑ jα je-τ∑ jaj, con un valor esperado ![]() [39].
[39].
Modelo de Gompertz
Cuando ya se pudo establecer claramente un aplanamiento en la curva de casos totales en Santiago, se ajustó un modelo de tipo logístico generalizado, el modelo de Gompertz, a la curva de casos totales(T(t)): ![]() (11). En este caso, a es la asíntota y b y c son los parámetros que controlan la posición de la curva y la tasa de crecimiento, respectivamente[41].
(11). En este caso, a es la asíntota y b y c son los parámetros que controlan la posición de la curva y la tasa de crecimiento, respectivamente[41].
Resultados
Modelo de máxima carga potencial
Este modelo reprodujo adecuadamente la forma de la curva epidémica, manteniendo valores por encima de los observados para casos semanales, número de unidades de cuidados intensivos ocupadas y número total de defunciones. Cuando los casos semanales se corrigieron por subregistro, se acercaron a las predicciones de carga máxima (Figura 1).
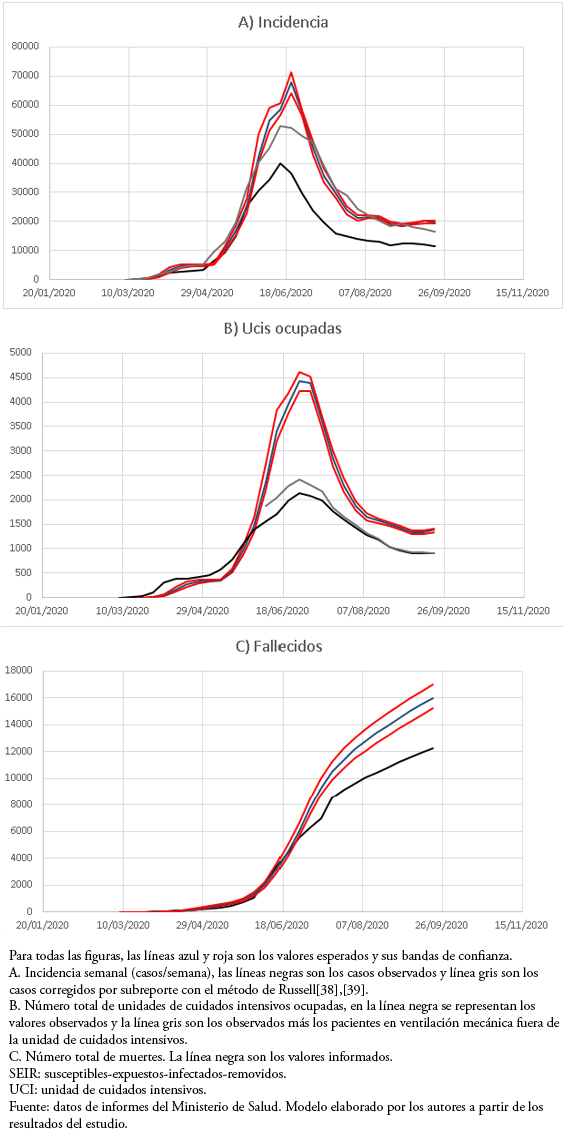 Tamaño completo
Tamaño completo Modelos SEIR discreto y modelo estocástico
Este modelo fue muy útil para predecir el aumento, el máximo de casos y la disminución de los casos, con gran poder predictivo hasta la fase de disminución del brote inicial en julio y principios de agosto (Figura 2A, Tabla 1). En los últimos meses se ha producido un mejor ajuste a los casos corregidos, pero se ha ido perdiendo ajuste especialmente en la ocupación de unidades de cuidados intensivos y el número de defunciones, lo que ha tenido importantes cambios en el sistema de notificación (Figura 2B, Tabla 1). El modelo estocástico SEIR permitió observar si las variaciones en el número de casos se debían a un desajuste en el modelo o a fluctuaciones aleatorias (Figura 2C).
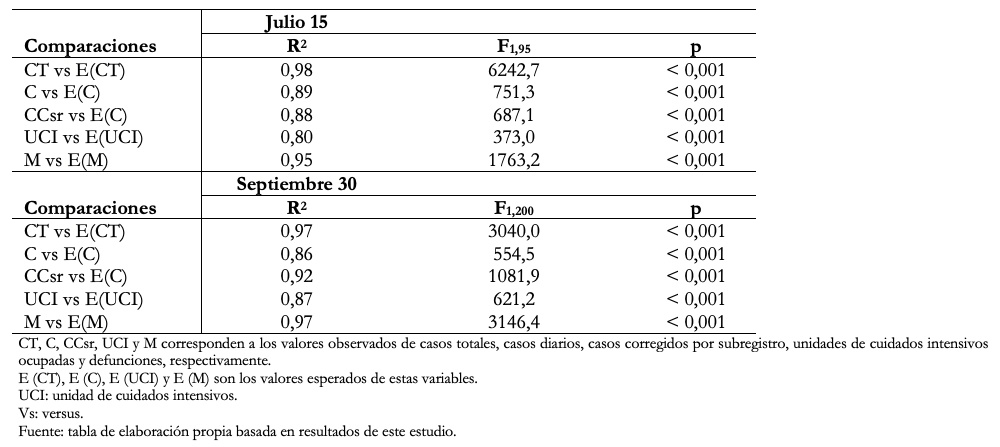 Tamaño completo
Tamaño completo 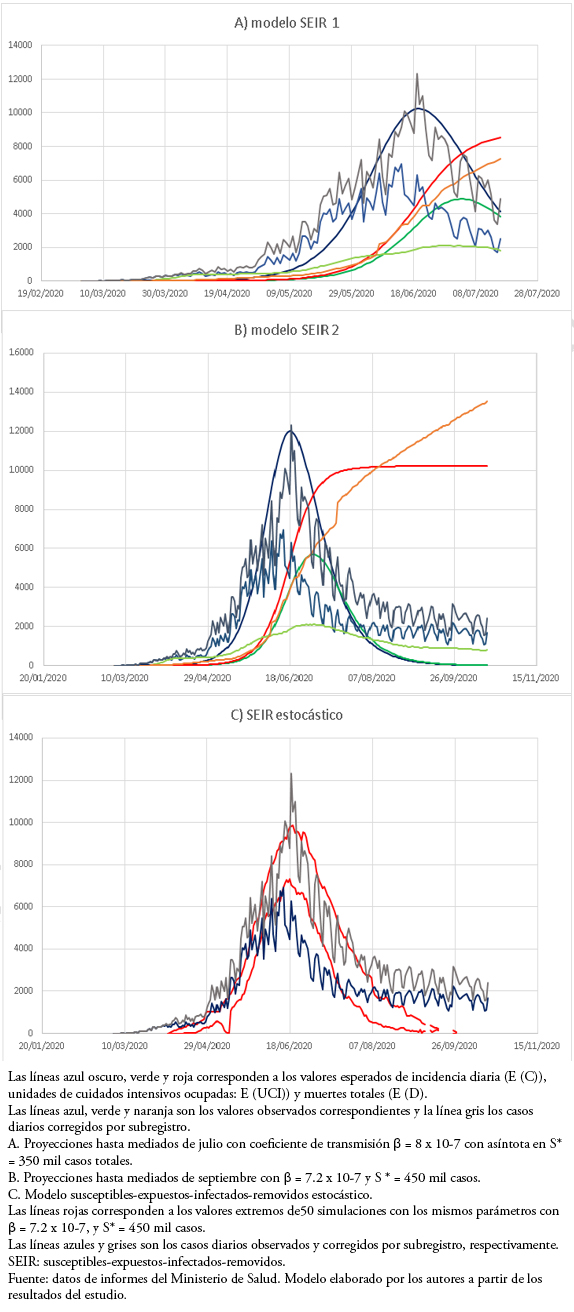 Tamaño completo
Tamaño completo Modelo de Gompertz para la Región Metropolitana (Santiago)
Este modelo ha permitido un buen seguimiento de la disminución del número de casos en la Región Metropolitana y, hasta el momento, una adecuada predicción de la situación endémica (Figura 3).
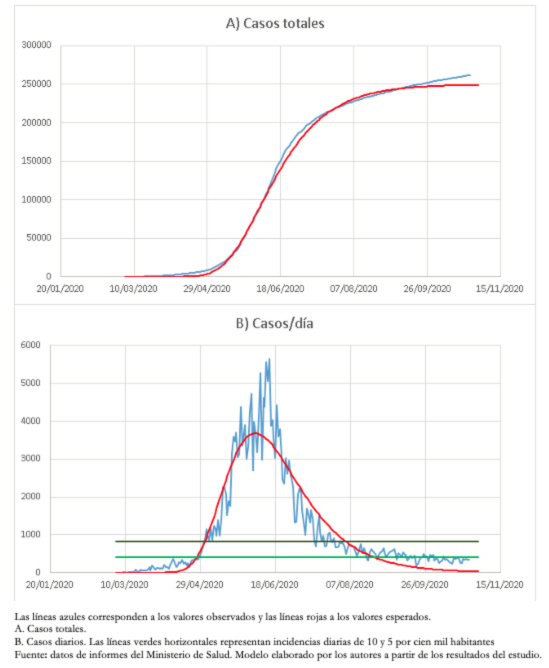 Tamaño completo
Tamaño completo Discusión
Los modelos matemáticos juegan un papel importante en el seguimiento de las epidemias, ayudando a racionalizar la toma de decisiones y a predecir eventos importantes en el curso de las epidemias, como el aumento, el máximo y disminución de la incidencia.
El objetivo del modelo de carga potencial máxima fue predecir la incidencia máxima, el número de unidades de cuidados intensivos ocupadas y las muertes en una semana. Inicialmente, mientras que la epidemia tenía números reproductivos muy altos, superiores a 1,5[33], los valores previstos eran muy similares e incluso inferiores a los valores observados para la incidencia y ocupación en unidades de cuidados intensivos. Sin embargo, después del 30 de mayo los valores predichos constituían un límite superior a los valores observados, permitiendo un coeficiente de seguridad adecuado en la predicción.
En cuanto a la incidencia, cuando se corrigió el número de casos por subregistro, que ha variado entre el 30 y el 60% a lo largo de la epidemia[33], los valores se acercaron bastante a los valores pronosticados con la excepción del máximo. La predicción de unidades de cuidados intensivos ocupadas en el período máximo fue muy superior a la observada, lo que se explica en parte porque durante el período máximo hubo una saturación de la capacidad de las unidades de cuidados intensivos, con hasta 400 pacientes en ventilación mecánica invasiva fuera de estas unidades. Hasta ahora, el modelo ha seguido adecuadamente la morfología de las curvas epidémicas, pero su capacidad predictiva es corta, solo una semana, lo que es similar a modelos anteriores desarrollados para la epidemia AH1N1 en Chile[13],[14],[15].
El modelo SEIR fue muy adecuado, con una excelente predicción del aumento, máximo y disminución del número de casos nuevos. Este modelo utilizó varios parámetros fijos que están bien justificados: periodo latente de 5 días[37], periodo infeccioso[38],[39], 3,5% de ocupación de las unidades de cuidados intensivos[42] y 2,6% de mortalidad[38],[39]. Además, considerar el 10% de los casos nuevos en relación con los casos activos resultó un supuesto adecuado, ya que al momento de la redacción de este estudio el porcentaje de casos nuevos notificados/casos activos fue de9,3 ± 4,9%. El coeficiente de transmisión se ajustó empíricamente utilizando al inicio 3,98 x 10-8 a principios de abril, prediciendo un máximo a comienzos de mayo. Posteriormente, el 15 de abril, se ajustó a 8 x 10-7 con una asíntota de 350 mil casos, con un excelente ajuste que predijo el máximo para el 19 de junio, el que ocurrió el 14 de junio.
También tuvo una buena predicción para la disminución inicial de casos. Además, hasta la última semana de junio tenía una predicción adecuada del número total de muertes. Sin embargo, la predicción de ocupación de camas estuvo muy por encima del número de unidades de cuidados intensivos ocupadas, lo que se explica en parte por la saturación ya mencionada. La disminución en el número de casos no siguió la curva típica de un modelo SEIR, lo que obligó a un nuevo ajuste en julio con β = 7.2 x 10-7, con una capacidad de carga de 450 mil casos. Ello mejoró el ajuste solo para dos semanas. Posteriormente, perdió toda capacidad predictiva desde principios de agosto. El modelo estocástico SEIR permitió incluir la variabilidad de las predicciones y mostró la misma pérdida de capacidad predictiva que el modelo determinista.
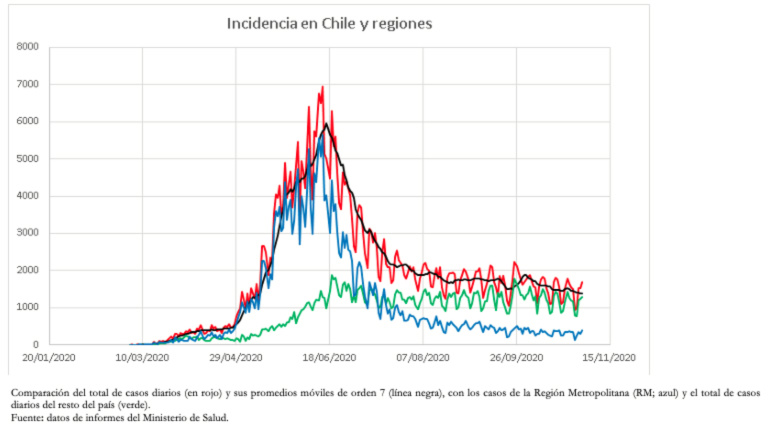
La buena capacidad predictiva del número de casos, la fecha de ocurrencia del máximo y también la pérdida de capacidad predictiva durante el declive de la epidemia de junio, se explican porque durante gran parte de la epidemia se produjo el aumento de casos y el número máximo de casos. Esto, principalmente por casos registrados en la Región Metropolitana (que incluye a Santiago), región que tiene una población de aproximadamente 8 millones de habitantes, alrededor del 42% de la población de Chile. Esta población está altamente intercomunicada, comportándose como una unidad. La disminución de casos en la Región Metropolitana ha coincidido con el aumento gradual y asincrónico de casos en las 15 regiones restantes, lo que ha mantenido los casos en un estado de alta endemia (Figura 4).
 Tamaño completo
Tamaño completo Como el descenso de casos en la Región Metropolitana fue asimétrico, se ajustó un modelo de Gompertz, que ha mostrado un muy buen ajuste en gran parte del proceso. Sin embargo, en los últimos días también ha ido perdiendo capacidad predictiva. Esto probablemente se explica porque la disminución en el número de casos no se ha producido de forma natural debido a la inmunidad colectiva, sino más bien asociada a una serie de intervenciones que han confinado a una gran parte de la población[33]. A la fecha de elaboración de este trabajo, la Región Metropolitana se encuentra en una etapa endémica relativamente estable de menos de 10 casos por cada cien mil habitantes.
Conclusión
De acuerdo a lo expuesto, los modelos utilizados han sido de gran utilidad, con diferentes objetivos en diferentes etapas de la epidemia. El modelo a corto plazo sigue siendo útil, ya que proporciona un límite superior en el número de casos por semana. Por su parte, el modelo SEIR tuvo una muy buena capacidad predictiva del máximo. En tanto, el modelo estocástico introdujo variabilidad en la predicción, y el modelo de Gompertz ha tenido una mejor capacidad predictiva del descenso de casos.
Notas
Roles de contribución
Conflictos de intereses
Financiamiento
Consideraciones éticas

