Notas metodológicas
← vista completaPublicado el 29 de agosto de 2018 | http://doi.org/10.5867/medwave.2018.04.7237
Índice para cuantificar la responsabilidad social individual en la decisión de vacunarse
An index to quantify individual social responsibility in the decision to be vaccinated
Resumen
En el contexto de estudios de enfermedades infecciosas genéricas, el objetivo del presente artículo es cuantificar y representar la responsabilidad social individual en relación al acto o no de vacunación individual. Aunque la finalidad de este análisis es meramente educativo y de divulgación masiva, el enfoque implementado está basado en el clásico modelo matemático Susceptible-Infectado-Recuperado (SIR) usando una estrategia impulsiva de vacunación. Día de vacunación y fracción de individuos vacunados son utilizados como parámetros del modelo, mientras que simulaciones numéricas son generadas para representar el comportamiento en la reducción de casos infectados a través de tablas y gráficos.
Ideas clave
|
Introducción
En los últimos años, se ha desencadenado un temor natural frente a los procesos sanitarios de inmunización mundialmente consolidados[1]. El referido estudio plantea un rechazo colectivo al proceso de vacunación, a consecuencia de un conflicto de interés entre profesionales de la salud, industria farmacéutica y medios de comunicación masiva. Lo anterior en particular hace referencia a un grupo de infantes del Reino Unido con variadas patologías y el suministro de la vacuna triple vírica correlacionada con la presencia de otras graves enfermedades.
Simultáneamente, ha comenzado a ser noticia los nuevos brotes de enfermedades infecciosas, que en general se tenían por controladas en diferentes partes del mundo[2],[3]. Entre ellas destacan los casos de sarampión registrados en Europa[4] y los recientes casos aparecidos en América Latina, región que se tenía por libre de este mal[5]. Aunque en Chile no se han reportado casos de sarampión desde 2016 a marzo 2018[6], los mitos y falsas creencias que nacen en el imaginario colectivo podrían perjudicar la óptima implementación de la vacunación como medida de prevención[7].
En los últimos años Chile ha realizado importantes esfuerzos sanitarios para que la población reciba las vacunas indicadas, entre ellos destacan los programas de vacunación contra la tos convulsiva[8] auspiciada por el Ministerio de Salud o la vacunación contra la influenza (2018)[9]. En el año 2017, autoridades de este ministerio, reportaron casos de coqueluche en la Región del Maule, ubicada en la zona central del país, con consecuencias graves entre la población de lactantes[10]. Esto originó un programa de vacunación inmediato a la población vulnerable de embarazadas por parte del cuerpo sanitario regional. Adicionalmente en el año 2018, se registraron nuevos brotes de parotiditis en la zona central y sur de Chile[11], lo que originó un reforzamiento en la red sanitaria y preventiva para mitigar las consecuencias.
Si bien es cierto que los procesos de vacunación contra enfermedades infectocontagiosas dependen de la autonomía individualista, varios investigadores subrayan la necesidad de someterlos a la ética de la responsabilidad social, encaminada al bien común[12]. Según los referidos autores el vacunarse o no, genera consecuencias no solamente de índole personal sino también de carácter social que podrían causar modificaciones en la cadena de contagios o generar cargas económicas para la sociedad. De esto, la población no siempre está consciente.
Tenemos la necesidad de educar a la población acerca de los beneficios de las vacunas, para erradicar enfermedades infectocontagiosas y para reducir las tasas de mortalidad en estratos más vulnerables. Lo anterior, mediante la aproximación de la población con argumentaciones múltiples y fundamentos diversos. En este sentido, el presente artículo pretende explicar con herramientas matemáticas, la responsabilidad social individualizada basada en la cuantificación de la disminución per cápita del número de contagios futuros asociados al acto de vacunarse, desde el instante de tiempo en que se aplica la vacuna. La metodología es una implementación del modelo matemático clásico de transmisión genérica con vacunación masiva en un tiempo puntual[13].
Mediante un indicador (función de los valores finales de las variables con y sin vacunación) y gráficas asociadas, entregamos una perspectiva analítica al problema. Se pone en evidencia la relación entre la prevalencia evitada (como número de individuos que no presentarán la condición de infeccioso) y las siguientes variables: la fracción de la población que es vacunada y el instante en que se efectúa esta vacunación.
Con el fin de evitar los tecnicismos y ganar en comprensión, nos situamos bajo un conjunto de supuestos que simplifican los cálculos, su análisis y presentación. La idea básica es considerar los efectos poblacionales (epidémicos) de un evento de inoculación único durante el desarrollo de una enfermedad infectocontagiosa, en comparación con la situación sin vacunación. Los aspectos más matemáticos, del todo evitables para el lector menos técnico, se han apartado en el apéndice.
La finalidad del presente artículo es introducir un indicador numérico, que denominamos indicador de responsabilidad social individual, para argumentar con herramientas matemáticas a priori el valor social de los procesos de vacunación, en particular cuantificar la disminución del número de contagiados futuros por individuo vacunado, desde el instante en que se aplica la vacuna.
De la enfermedad y la vacunación
Consideramos el caso de una enfermedad infectocontagiosa genérica, de fácil y rápido contagio, provocada por el alojamiento de algún agente patógeno (virus o bacteria), que en el periodo observado produce inmunidad (sin reinfecciones). Estamos situados, por ejemplo, en algunos de los tipos de influenza, en que la propagación es por la aproximación o el contacto físico de una persona sana con otra infectada, a través de la exhalación y posterior inhalación de microgotas[14] Supondremos también que la enfermedad es suficientemente rápida como para obviar la dinámica demográfica (nacimientos y muertes). Además, se asume que el período de desarrollo los parámetros asociados a los procesos de contagio y recuperación tienen un comportamiento uniforme. Por ejemplo, la probabilidad de contagio no cambia por las condiciones abióticas existentes y además, afecta por igual a los distintos grupos territoriales, de edad y/o género.
Modelo de la dinámica de la enfermedad
Generamos un escenario (modelo) que recoge lo grueso de los procesos de contagio y recuperación, pero que desdeña los detalles de una enfermedad, población y entorno específico.
En este sentido, asumimos que la dinámica básica de la enfermedad implica que una persona solo puede presentar uno y sólo uno de tres estados consecutivos. Estar inicialmente sano, pero susceptible (S) de enfermar, luego enfermar y rápidamente tener el potencial de contagiar a otros, que denominamos estado infeccioso (I) y que dura un período de tiempo, para finalmente salir de dicho grupo con inmunidad, esto es, estar recuperado (R). El paso no reversible por estos tres estados. Lo diagramamos del modo siguiente:
Susceptible →(α) Infeccioso →(β) Recuperado
En el ámbito de la epidemiología matemática, lo anterior corresponde al modelo que se denota SIR, un caso muy particular de la teoría de Kermack – McKendrick[15],[16],[17]. De manera simplista, básicamente se trata de un flujo unidireccional S I R, sin retroalimentaciones, de personas por tres compartimentos consecutivos. En el inicio, o previo a la aparición de la enfermedad, todos se encuentran en el primer estado conceptual (S), luego algunos de estos, los contagiados, pasan por el segundo (I) durante un período tiempo, los que necesariamente terminan en el tercero (R), sin posibilidad de reinfectarse. Notemos que el cambio de condición no es simultáneo al grupo, sino a través de tasas, una proporción por unidad de tiempo.
El flujo (a): S→I, se expresa basándose en cómo ocurre el contagio. Acá, el modelo supone que los individuos no cambian mayormente su dinámica social por la presencia de la enfermedad, de modo que, en cada momento la proporción de encuentros cercanos que pudieran generar contagio no cambia en el tiempo, como tampoco la capacidad y las condiciones para que un agente infeccioso se traslade de un hospedero (un infeccioso) a un hospedero nuevo (un susceptible). En otras palabras, diariamente existe un porcentaje fijo de susceptibles que cada infeccioso es capaz de contagiar. Denotemos este porcentaje por B%. Así, cada día el flujo (a), denominado incidencia, está dado por:
Incidencia = B%× n° Susceptibles × Infecciosos,
donde el signo X indica, como es usual, multiplicación.
En cuanto a (b): I→R, la recuperación, esto es el paso desde la condición de infeccioso hasta recuperado, asumiremos que en el proceso de la enfermedad se determina que en promedio un infeccioso está T días como un trasmisor del agente patógeno subyacente. Entonces, por cada día es removida una fracción 1/T de los infecciosos. En otras palabras, el flujo (b), denominado tasa diaria de recuperación, está dado por:
Tasa de recuperación =(1/T)× n° Infecciosos
Supondremos que en una población sana de N individuos, todos susceptibles, en el día cero de la enfermedad arriba una persona recién infectada (por ejemplo, un turista retornando al país) que por transmisiones sucesivas gatilla el desarrollo de una cadena de contagios. Simplificando, además asumiremos que la población se cierra, por ejemplo por alguna regulación interna y mecanismo de detección temprana, a la entrada de nuevos contagiados. Entonces, la enfermedad tiene una opción de propagación solo cuando el caso primero es capaz, mientras permanece en su condición de infeccioso, de dejar uno o más casos secundarios. En epidemiología matemática, este número de nuevos infecciosos se denomina el número reproductivo básico, el cual es denotado generalmente por[18],[19]. Notemos que su cálculo formal para este modelo está determinado por la siguiente fórmula:
R0=B%×N×T.
La que es posible leer como el contagio diario de un infeccioso dentro de N susceptibles (B%×N), multiplicado por el número de días T que éste permanece contagiando.
Modelo de la dinámica de la vacunación
En orden a visualizar el efecto de la vacuna en la prevalencia, consideraremos que al d-ésimo día se procede a inmunizar, por única vez, un p% de la población susceptible en dicho instante. También se considera que los efectos de dicha inmunización son instantáneos, es decir, las personas integran de inmediato el grupo vacunados (V). Entonces, este flujo se expresaría como:
Susceptibles →(C) Vacunados
Lo expuesto aquí, determina una remoción al d-ésimo día de introducida la enfermedad en la población, igual a:
p%× n° Susceptibles.
En resumen, al comienzo (día cero) toda la población N es susceptible de ser contagiada, momento en el que ingresa un primer infeccioso, a partir del cual se desencadena un proceso de contagio, generando nuevos infecciosos que son agentes transmisores durante un periodo de T días. Entonces, al d-ésimo día, la agencia de salud implicada, procede a vacunar un p% de los no contagiados a ese día, los susceptibles. A partir de lo anterior, surgen las siguientes preguntas:
- ¿En cuánto disminuyó, al final del brote, el número de personas que en algún momento enfermó?
- ¿Cuánto aportó cada vacunado a esta disminución?
Resultados
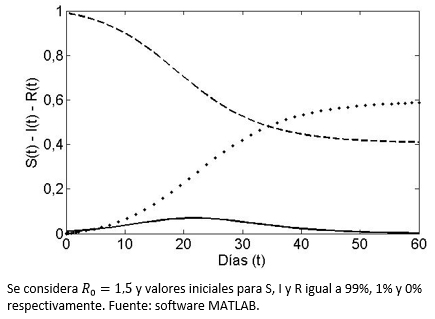
Los flujos descritos en detalle en la sección anterior han sido programados computacionalmente, a través del software MATLAB (pudiendo haber sido cualquier otro), con parámetros numéricos específicos. Notemos que se asume que al principio de la enfermedad y en promedio dos infecciosos logran dejar tres nuevos infecciosos antes de sanar (R0=1,5, valor aplicado, por ejemplo, a la gripe de la pandemia H1N1-2009)[20]. Se establece además que inicialmente el 1% es infeccioso y que el restante 99% es susceptible de enfermar. En la Figura 1 se grafica en línea continua el porcentaje que representa el grupo infeccioso del total de la población, de no existir un evento de vacunación. La curva sin vacuna (sv) es siempre unimodal (se expresa el brote) con una caída asintótica a cero al transcurrir el tiempo, es decir, la enfermedad deja la población, lo que simbolizamos ![]() . Nótese que el máximo de personas infecciosas es de un 7% y se alcanza aproximadamente al día 22 de la enfermedad. El caso para las curvas de los grupos susceptibles (línea segmentada) y de recuperados (línea punteada) es respectivamente de decrecimiento a un valor final
. Nótese que el máximo de personas infecciosas es de un 7% y se alcanza aproximadamente al día 22 de la enfermedad. El caso para las curvas de los grupos susceptibles (línea segmentada) y de recuperados (línea punteada) es respectivamente de decrecimiento a un valor final ![]() positivo (no todos terminan contagiados) y de crecimiento asintótico a
positivo (no todos terminan contagiados) y de crecimiento asintótico a ![]() (total de individuos que estuvieron contagiados en algún momento). Estas últimas tienen respectivamente siempre una forma sigmoidea y de sigmoidea inversa.
(total de individuos que estuvieron contagiados en algún momento). Estas últimas tienen respectivamente siempre una forma sigmoidea y de sigmoidea inversa.
 Tamaño completo
Tamaño completo Tiempo de vacuna
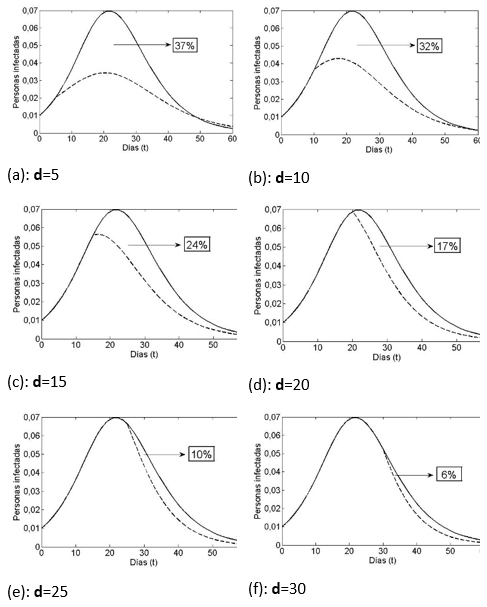
Al considerar el caso con vacunación (cv), al d-ésimo día, en las gráficas de la Figura 2, a través de las líneas segmentadas podemos ver el efecto de reducción del grupo infeccioso. Sin embargo, una jornada de vacunación antes de los 22 días lograría reducir ese tope aproximadamente al 3,3%; 4,2% o 5,6%, según se vacune respectivamente al quinto, décimo o décimo quinto día, casos (a)-(c). Una vacuna cerca de los 22 días o después, casos (d)-(f), no hace mayor diferencia en esta prevalencia máxima.
Notemos que el tiempo que transcurre entre el caso cero y el instante de aplicación de la vacuna, determina un efecto importante sobre el número de personas que finalmente tuvo la enfermedad.
En la Figura 2 se representa el efecto sobre el tamaño del grupo de infecciosos, de vacunar un mismo porcentaje (15%) del grupo susceptible, pero en distintos días. Es claro, que a una vacunación más temprana le corresponde una disminución mayor en el número de los que alguna vez se enfermaron. El área bajo la gráfica (salvo un factor 1/T) es una medida justamente de la cantidad de personas que en algún momento estuvieron afectadas. Vemos que al avanzar en las gráficas de la Figura 2 de (a) a (f), la diferencia de áreas, bajo la curva en línea continua (sin vacuna) y sobre la curva en línea segmentada (con vacuna) se va anulando, es decir, el beneficio de la vacuna se va perdiendo al pasar de los días.
 Tamaño completo
Tamaño completo Notemos que al final del brote el haber vacunado producirá menos gente contagiada, un indicador interesante es conocer por cada vacunado cuántas personas menos no se habrán contagiado, es decir, a parte del beneficio personal de quien se vacuna (no enfermar) a cuantos otros se favorece, esto es, la idea de un indicador de responsabilidad social individual. Este mide la reducción de contagiados por vacunado y le simbolizamos con . Así, este indiciador se calcula como el número final de infecciosos evitado, que es la diferencia entre: el número final de infecciosos recuperados de no haber vacunación ![]() y esta cifra, pero con vacunación
y esta cifra, pero con vacunación ![]() , dividido por el total de vacunados . Entonces:
, dividido por el total de vacunados . Entonces:
![]()
Se observa, tanto en la Tabla 1 como en el gráfico de la Figura 3, que una vacuna temprana favorece la reducción en el número final de personas afectadas directamente. Por ejemplo, vacunar a los cinco días del ingreso de la enfermedad, un vacunado no solo evita enfermarse él, sino aporta en 1,5 contagiados menos. Este efecto, se va reduciendo con el tiempo, entre los 25 y 30 días se requerirían tres vacunados para el mismo efecto. Del día 50 en adelante prácticamente no se evitan otros contagiados, salvo la probabilidad individual.
 Tamaño completo
Tamaño completo 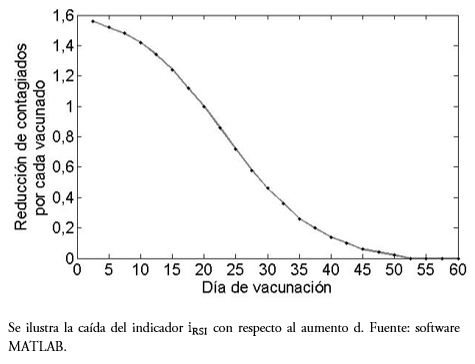 Tamaño completo
Tamaño completo Fracción vacunada
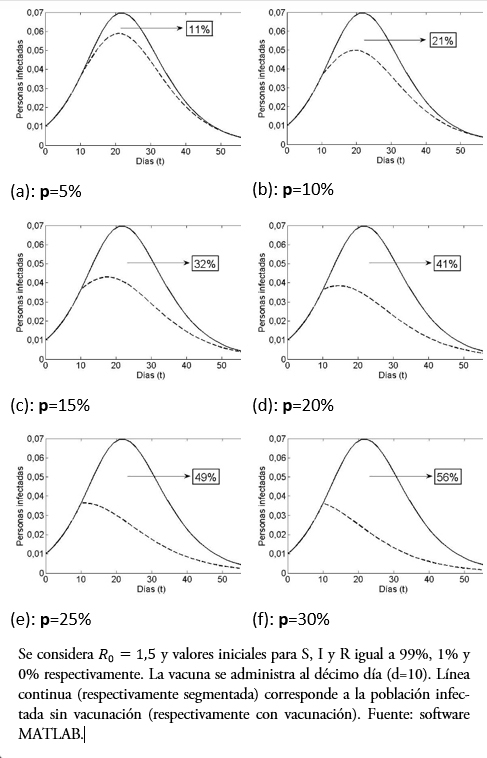
Otra pregunta interesante es ¿qué comportamiento tiene al indicador si, fijando el día de vacunación, se varía el porcentaje p de personas inmunizadas? Lo observado en las gráficas de la Figura 4 muestra claramente la diferencia. En efecto, estas gráficas comparan la población infectada versus días, pero variando la fracción de vacunados al décimo día, desde un 5% en (a) hasta un 30% en (f), se entiende de la población susceptible en ese día. El porcentaje, logra disminuir la curva de infecciosos (línea segmentada). Por otro lado, se puede observar desde la Tabla 2 y la gráfica de la Figura 5, que la reducción de contagiados por vacunado disminuye al aumentar la fracción de vacunados (lo cual parece contradictorio), pero esto ocurre debido a que, tras aumentar la población susceptible vacunada, disminuirá la infectada. Sin embargo, entre menos porcentaje de la población se vacune mayor es la responsabilidad individual, aunque el rango de variación [1,32; 1,45] es estrecho, para nuestros valores de parámetros.
 Tamaño completo
Tamaño completo  Tamaño completo
Tamaño completo 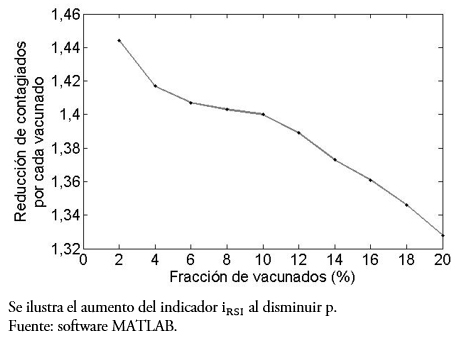 Tamaño completo
Tamaño completo Conclusión
Mediante un modelo matemático muy simple de propagación de una enfermedad infectocontagiosa y control por inmunización, este artículo otorga respaldo y complementa, desde una perspectiva analítica, los esfuerzos formales asociados a realzar, como medida precautoria de brotes epidémicos, la importancia estratégica que tienen las campañas de vacunación y el que éstas se desarrollen a tiempo. En efecto, se cuantifican e ilustran las consecuencias del acto de vacunación al cortar las posibles cadenas de contagio tras el paso del brote. En esta línea es fundamental el conocer, por ejemplo, la reducción en el número de personas que alguna vez fue contagiada.
Como es de esperar, cada trayectoria determinada por el sistema dinámico tipo susceptible – infectado – recuperado considerado, es alterada en forma impulsiva con un evento de vacunación (retiro instantáneo de una fracción del grupo susceptible), la prevalencia total final (fracción de la población en algún momento contagiada) disminuye. Sin embargo, esta reducción es menor tanto si la vacunación es tardía como si el porcentaje de inoculados es menor (ver demostración en el apéndice).
Más precisamente, dada una enfermedad contagiosa (que ajusta a un modelo tipo susceptible – infectado – recuperado, con parámetros de contagio y recuperación constantes) se logró ilustrar en cuánto disminuye el número de personas que en algún momento enferma por cada individuo vacunado. Así, se muestran para distintos instantes y porcentajes de vacunación, las consecuencias en términos de cuántas más personas no se enfermarán el que alguien sea vacunado, esto cómo un indicador en positivo. Notemos que una persona al no vacunarse no solo se pone él en riesgo, sino que de seguro, es el responsable del contagio de otros. He aquí, la responsabilidad social que existe tras la decisión de un individuo, una incumbencia que de algún modo u otro similar, es medido por el indicador .
En síntesis, la novedad de este artículo está en el enfocarse no sólo en la obvia responsabilidad de la sociedad, sino poner en manifiesto también la perspectiva individual. Como vemos, además hemos sumado argumentos para que comprometamos al Estado con un accionar oportuno y con mayores coberturas en las vacunaciones masivas.
Notas
Roles y contribuciones de autoría
FCL: conceptualización, metodología, análisis formal, investigación, redacción (revisiones y ediciones), supervisión, administración del proyecto. JPGJ: metodología, investigación, gestión de datos, presentación de datos, preparación de manuscrito (desarrollo del borrador original), visualización. MTMQ: conceptualización, investigación, redacción (revisiones y ediciones).
Fuentes de financiamiento
Los autores declaran que no hubo fuentes de financiación externas.
Declaración de conflictos de interés
Los autores han completado el formulario de declaración de conflictos de intereses del ICMJE, y declaran no haber recibido financiamiento para la realización del reporte; no tener relaciones financieras con organizaciones que podrían tener intereses en el artículo publicado, en los últimos tres años; y no tener otras relaciones o actividades que podrían influir sobre el artículo publicado. Los formularios pueden ser solicitados contactando al autor responsable o a la dirección editorial de la Revista.
Agradecimientos
Agradecemos a la línea de Análisis Epidemiológico del programa de Doctorado en Modelamiento Matemático Aplicado, Universidad Católica del Maule. Además, al equipo de investigadores del proyecto FONDECYT de Iniciación #11150784.
Anexo
Material suplementario disponible en https://doi.org/10.6084/m9.figshare.7022180

