Notas metodológicas
← vista completaPublicado el 28 de diciembre de 2018 | http://doi.org/10.5867/medwave.2018.08.7396
Modelización del impacto epidemiológico de la existencia de un grupo conductual preventivo
Modeling the epidemiological impact of a preventive behavioral group
Resumen
En lo que concierne a salud, la experiencia indica que en toda población humana existe un porcentaje de individuos que se comporta en forma consciente ante la presencia de enfermedades infectocontagiosas. Esto implica que existen grupos con una orientación hacia la prevención en sus actividades para atenuar el riego, mientras que en general la mayoría lo hace distraídamente. La excepción la constituyen los casos de orden catastrófico. Asumiendo el marco teórico y metodológico que otorga la epidemiología matemática, se evaluaron los factores tamaño e intensidad de la conducta del grupo cuidadoso en la determinación del número reproductivo básico, basándose en un modelo tipo SIR (susceptibles - infecciosos - recuperados). Es decir, se midió la reducción en la cantidad de casos secundarios que produciría un primer caso infeccioso. Junto con estos indicadores, se procedió a evaluar la prevalencia evitada total e individual por cada sujeto cuidadoso en diferentes escenarios paramétricos. Finalmente, se plantea la necesidad de integrar en futuros estudios la variable distancia y el contacto interpersonal como factores asociados al potencial de transmisión.
Introducción
Las nuevas realidades, ritmos y movimientos en la dinámica social exigen la incorporación en los modelos epidemiológicos de enfermedades infectocontagiosas humanas de escenarios más realistas. Un aspecto a considerar es que estos modelos sean capaces de capturar la diversidad de conductas de los individuos para luego, desde el modelo mismo, conocer las consecuencias en las predicciones[1],[2]. Sin embargo es necesario, en términos del tránsito del análisis a la síntesis, incorporar primero los diversos aspectos por separado y posteriormente intentar mayor complejidad mediante la integración de dichos fenómenos.
Según expertos, las formas de comportamiento humano para evitar el riesgo en salud están condicionadas por un extenso número de factores, entre los que destacan creencias religiosas, culturales y nivel socioeconómico, entre otros[1],[3]. De allí que en todo grupo social existan niveles individuales que responden a circunstancias muy personales con respecto a sus patrones de conducta, según se plantea en los mencionados trabajos.
De acuerdo a la lógica natural, ante riesgos de infección, algunos individuos se comportan distraídamente o cambian en forma muy parcial sus actividades; mientras que otros, más conscientes, prefieren las actividades claramente orientadas a la prevención y el control del contagio[1]. Es decir, las personas nos dividimos en al menos dos patrones de conducta ante algún indicio de epidemia. Podemos afirmar que la dinámica general de desarrollo de las enfermedades es bastante sensible al comportamiento individual y a la dimensión que alcanzan estos como grupos sociales.
En aras de mejorar los índices, el llevar personas de un grupo a otro implica lograr cambios de estilos de vida en individuos (sanos y/o enfermos) que están enmarcados dentro de una variedad de modos de vida. Se requieren cambios de paradigma social y psíquico que van más allá de aspectos meramente biológicos, sociales o culturales, ya que involucran aspectos de personalidad y grados de equilibrio psicosociales. No obstante, todo cambio social requiere alcanzar cierto número umbral de personas en la conducta adecuada. Por otro lado, aunque una persona en su actuar esté consciente de la buena o mala conducta en salud, quizás no siempre está instalada en ella una más definida visión del alcance (consecuencias) de sus acciones.
Tener ciudadanos educados y responsables en sus costumbres sanitarias es de vital importancia para el sistema de salud de las comunidades, en particular en lo referente a la prevención y mitigación de enfermedades. Sin embargo, no siempre es posible encontrar en la literatura argumentos que intenten cuantificar cómo un grupo poblacional conductual hace la diferencia al respecto. Por ejemplo, en lo relativo al efecto que tiene en la propagación de enfermedades infectocontagiosas una conducta estándar versus una particularmente cuidadosa. En principio, hay dos formas (conjugables) para introducir cierto nivel de cuantificación de las consecuencias:
a) Modelo estadístico: que recurre a los datos (existentes o por experimentar), con situaciones con y sin conducta específica. Verbigracia, un trabajo conducido en China sobre patrones sociales mixtos en zonas urbanas y rurales[4] o modelado del espacio personal[5] a través de una función Gaussiana Bidimensional.
b)Modelo matemático: mediante la introducción de hipótesis relativas a la conducta sobre el modelo epidemiológico base de una enfermedad infectocontagiosa, realiza análisis y/o simulaciones del mismo. En este caso, un trabajo sobre modelos matemáticos de patrones de contacto en grupos de edades[6] o más recientemente un modelo epidémico susceptible- infeccioso-susceptible con población cuidadosa, donde se investiga el retardo en la respuesta de cuidado por parte de la población susceptible[7].
En este sentido, con la idea de introducir medibles, la dinámica del comportamiento humano y sus consecuencias epidemiológicas, podría estar mejor representada desde la perspectiva metodológica de los modelos matemáticos[6],[7],[8]. En particular los compartimentados y las leyes de variación del tamaño de los mismos, con una definición clara que incluya características o tipos conductuales y las reglas específicas de transferencia para los individuos que conforman cada grupo[1],[2],[6]. En consecuencia, el desafío clave es establecer las líneas bases de conducta para su incorporación al modelo. Notemos que estos tipos de conductas se traducen en mayor o menor probabilidad de traspaso del agente infeccioso a un nuevo hospedero.
El propósito del presente artículo es poner en relieve, a través de un modelo matemático (sistema dinámico determinista) y posterior construcción de indicadores específicos, la importancia que tiene la existencia y tamaño de los grupos conductuales en el desarrollo de modelos epidemiológicos para enfermedades infectocontagiosas. Para ello se cuantifica el impacto epidemiológico que tiene dicha heterogeneidad sobre la condición susceptible o infecciosa de los individuos, con proyección en la prevalencia. Una vez identificados y cuantificados estos aspectos, podría convertirse en una herramienta útil, grosso modo, para guiar políticas públicas sanitarias destinadas a mitigar los efectos en salud a través de cambios conductuales humanos.
Objetivos
En el contexto específico de una enfermedad infectocontagiosa con potencial para una rápida propagación, que pudiera generar un no despreciable brote (pulso) epidémico, como podría ser el caso de una gripe; esta investigación se orienta a responder las siguientes incógnitas:
- ¿Cuánto y cómo impacta en la magnitud de la prevalencia final (alguna vez enfermos) la existencia de un grupo de personas en la población con conductas cuidadosas, ante una enfermedad transmisible?
- ¿Cuál es la ganancia o pérdida, es decir menor o mayor prevalencia, al aumentar o disminuir el número de personas con conductas preventivas, en términos relativos respecto al total poblacional?
- ¿Entre sociedades con características ambientales similares (asociadas con la enfermedad), existen diferencias significativas entre la existencia de individuos levemente cuidadosos o por el contrario individuos altamente cuidadosos?
- ¿Qué tipo de persona cuidadosa impacta más positivamente, el susceptible de enfermar o el sujeto como agente infeccioso?
Tipos conductuales
En toda sociedad existe un grupo de ciudadanos conscientes que toman medidas preventivas sanitarias, tanto a favor de ellos mismos (cuando aún no han sido infectados) como con respecto a sus pares o círculos de contacto (cuando ellos cargan con la condición infecciosa). Este conjunto lo hemos denominado como “grupo cuidadoso”, y por simple complemento el resto de la población se ubica en el “grupo estándar”. Es importante destacar que, para efectos de gestión preventiva, resulta lógico esperar que sea favorable el conocer cuál es el impacto que tiene en la salud de la población (respecto a un grupo u otro) el ganar más ciudadanos en la condición de consciencia cuidadosa como medida sanitaria; sin embargo, nuestro objetivo es cuantificarlo.
La identificación de un grupo cuidadoso se relaciona con el conocimiento, conciencia y actitud epidemiológica permanente de un sector de la población frente a las prácticas básicas destinadas al control y prevención de enfermedades infecciosas transmisibles. En este sentido, aspectos como los descritos en documentos tales como el Manual de Control y Prevención de Infecciones[9], podrían ayudar a delimitar la pertenencia o no de un sujeto a este grupo. Más precisamente, nos referimos a cierto nivel de cumplimiento observable de estándares de elementos como higiene de las manos, aislamiento, higiene respiratoria, normas educativas al toser, desinfección y lavado de utensilios personales u otras.
Ante una enfermedad infectocontagiosa junto a dos zonas similares en lo ambiental y demográfico, nos preguntamos las razones por las cuales podrían existir diferencias sustanciales en el tamaño final de una infección. Un factor social explicativo, pudiera ser la existencia de mayor masa de individuos que mantienen y/o activan conductas de cuidado permanentemente o más específicamente ante la aparición de brotes epidémicos. Sin embargo, para saber hasta dónde resiste esta hipótesis, es necesario medir cuán grande puede ser esta diferencia. Por razones obvias, en el presente estudio no se aborda un escenario experimental, sino uno simulado. De allí que se requiere la construcción de un modelo matemático que permita, en términos de una realidad simplificada con bordes definidos, efectuar los análisis requeridos. Para ello consideraremos como base un modelo matemático clásico de compartimentación (susceptible - infeccioso - removido), ampliamente usado en el análisis epidemiológico[10], sobre los cuales alojaremos algunos supuestos:
- La población, además de estar compartimentada según los estados de la enfermedad, también lo está según el tipo de conducta del conjunto al que pertenecen los individuos que la conforman, siendo ellos: grupo estándar (E) o grupo cuidadoso (C).
- Los grupos E y C representan un porcentaje dentro del total poblacional, denotados respectivamente por QE% y QC%, donde QE% + QC% = 100%. Estos porcentajes en el curso de la enfermedad se considerarán fijos.
- La probabilidad de encuentro o contacto inter e intragrupal será la misma. La diferencia estriba en la probabilidad de que estos contactos sean efectivos o no para que ocurra el contagio. Además, asumiremos que un cuidadoso (C) disminuye dicha probabilidad en un factor que denotamos respectivamente por fS y fI y, con fS,fI ∈[0,1] , según el cuidadoso actúe como susceptible o infeccioso.
Dinámica de la enfermedad
Aunque intentaremos evitar en lo posible el tecnicismo matemático, los detalles argumentativos y cálculos formales propios de esta disciplina se exhiben en la sección final. En este contexto, la argumentación estará basada en diagramas, tablas y algunas gráficas producto de simulaciones numéricas.
Bajo supuestos epidemiológicos de uniformidad espacial y etaria, uno de los clásicos modelos matemáticos de enfermedades infectocontagiosas, asume tres grandes grupos de individuos: susceptibles, infecciosos y recuperados[6]. Vistos sus tamaños como variables dependientes del tiempo, al -ésimo día de la enfermedad a partir de la llegada al sistema de un número inicial de infecciosos (día cero), su representación se denotará por S(t), I(t) y R(t) respectivamente.
En relación con la distancia que mantienen dos o más personas (variable discutida en detalle en la siguiente sección “distancia y contacto interpersonal”), se puede definir un criterio para discriminar si estas personas se encontraron (contactaron) o no. Para ello, notemos que la cantidad de encuentros factibles entre un individuo del grupo susceptible y otro del grupo infeccioso está representada por el producto S(t)I(t). Efectivamente, solo una fracción de estos encuentros ocurre realmente. Más aún, ocurren solo en una fracción de esta última, cuando exista una distancia adecuada que permita la posibilidad que el agente patógeno cambie de hospedero. A su vez, esta situación se da solo con cierta probabilidad, la cual depende de muchas variables, entre ellas cuán prolongado es el encuentro para que llegue a ocurrir el contagio. En definitiva, solo en una pequeña fracción de los encuentros factibles entre susceptibles e infeccioso, el susceptible termina siendo infectado. Notemos que una limitante de estos modelos (susceptible - infeccioso - recuperado), es la no existencia de un periodo de latencia. Esto es, de haber contagio, instantáneamente se pasa a la condición de infeccioso.
Como ha sido dicho implícitamente, un modelo susceptible - infeccioso - recuperado asume dos flujos básicos: el de infección (S→I) y el de recuperación (I→R). Para el flujo de infección supondremos que por unidad de tiempo (un día) cambia de compartimento la suma de B%S(t)I(t) susceptibles (un infeccioso infecta el B% del grupo susceptible). En cuanto al de recuperación, si el tiempo promedio de permanencia es de T -días, por unidad de tiempo se recuperan (1/T)I(t) individuos infecciosos. Más detalle pueden ser encontrados en Córdova-Lepe, 2018[10].
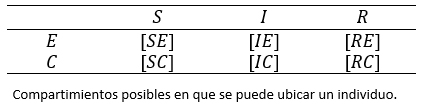
En la Tabla 1 se ilustran los tipos de encuentros posibles. Es decir, se consideran las posibilidades de perfiles que puede tener una persona al cruzar los tipos infecciosos con los tipos conductuales .
 Tamaño completo
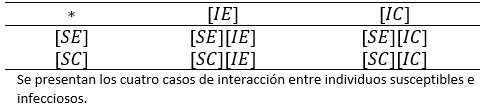
Tamaño completo De este modo, si las expresiones [XY] de la tabla anterior indican el número de individuos en dicha condición, entonces los encuentros posibles entre personas susceptibles e infecciosas quedan representadas en la Tabla 2.
 Tamaño completo
Tamaño completo La Tabla 3 muestra los cuatro componentes del flujo S→I, es decir, el número de nuevos infecciosos por unidad de tiempo. Estos valores se expresan según la Tabla 2 y en términos de la tasa de contagio corregida por los factores de reducción asociados al grupo cuidadoso.
 Tamaño completo
Tamaño completo Notemos que hemos supuesto que una persona al infectarse no cambia su tipo de conducta, por lo que si era del tipo [SX], cualquier X entre los dos posibles casos (X∈{E,C}) y se infecta, este se integrará al grupo [IX]. Es decir, el mismo X con el mismo tipo conductual. Así, genéricamente X -fila indica cómo los susceptibles tipo X se infectan con los distintos tipos infecciosos. O sea, el flujo hacia infecciosos estándar y cuidadoso son respectivamente:
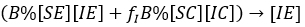
y
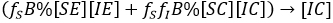
Factorizando, resulta:
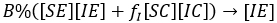
y
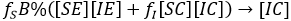
El flujo se completa considerando la recuperación [IX]→[RX] para cada tipo conductual X∈{E,C}. El tiempo de recuperación supuesto (independiente al tipo conductual), es de (1/T)[IX] personas por unidad de tiempo. Como los removidos no participan más en la dinámica del contagio, podemos pensar en un solo grupo de removidos [R]=[RE]+[RC].
Estos dos flujos determinan la ley de desarrollo de la enfermedad infectocontagiosa, la cual se expresa matemáticamente como ley diferencial según la ecuación planteada en la sección “elementos matemáticos”.
Distancia y contacto interpersonal
Los factores fS y fI, llamados de reducción de la tasa de contagio, están asociados a la probabilidad de trasmisión del agente patógeno. El número de contagios es sensible a los patrones de aproximación y contacto humano[1],[6]. En relación a la neumonía, por ejemplo, un estudio histórico con datos de las epidemias de peste neumónica (Manchurian, años 1910-11 y 1920-21), muestra que al toser existe riesgo epidemiológico para distancias entre cinco centímetros a dos metros[11]. Consabidas recomendaciones para evitar la exposición a las gotas de saliva que genera un enfermo al toser o estornudar, son el taparse la boca y también el uso de mascarillas[12].
Las distancias que empleamos en nuestro diario vivir, en relación con otros sujetos y objetos son materia de estudio de la proxémica (Edward Hall, 1968)[13]. El espacio personal (burbuja alrededor del cuerpo humano) que una persona mantiene respecto a otra en sus relaciones diarias, tiene importancia epidemiológica y determinantes tan diversos como personalidad, edad, género, condición social, tipo de relación entre pares[5] y contextos culturales[13],[14].
Dicho espacio personal está configurado por varias capas, según ciertas distancias (íntima de 0 a 0,45 metros; personal de 0,45 a 1,2 metros; social de 1,2 a 3,5 metros y pública a más de 3,5 metros) de acuerdo con el tipo de interacción con otros[5]. Según se observa, algunas capas están dentro de la zona de riesgo para la peste neumónica. Por lo que se espera que una persona cuidadosa, interactúe con el medio a través de capas con promedios de distancia mayores, lo que determinaría valores de fS y fI menores.
En este sentido, la proxémica advierte que el diámetro de las capas cambia según la cultura, lo que podría ser un factor para explicar diferencias entre procesos de transmisión de enfermedades infectocontagiosas. Los angloamericanos por ejemplo, tienden a interactuar socialmente con distancias mayores que la de los latinos; estos últimos además incluyen el contacto físico[14]. Adicionalmente, según el mencionado trabajo, existen diferencias de contacto y acercamiento social entre miembros de países latinos y entre encuentros de géneros. De allí que no habría un índice único (universal) de contacto humano común para todas las culturas, ni dentro de las mismas[13],[14].
Existen evidencias que para muchas infecciones, la transmisión del agente patógeno ocurre en relación con la distancia que mantienen los sujetos entre sí[4],[11]. En un estudio conducido en Gran Bretaña[15], se registró un trabajo con enfoque estadístico en el cual la probabilidad de contagio entre susceptibles e infecciosos disminuye con la distancia, de acuerdo con la formulación de la Ley de Potencia. Más precisamente, se determinó para contagio de la fiebre aftosa entre granjas, que la probabilidad de contacto escalaba según la lejanía. En consecuencia, la transmisión del contagio entre el ganado resultó inversamente proporcional a la distancia entre granjas.
Otro estudio reciente conducido en Bangladesh, con datos de Chikungunya, incorporó una distribución exponencial para caracterizar la probabilidad de transmisión entre comunidades y su distancia de separación. En esta investigación se analiza cómo las estructuras sociales, espaciales y la dinámica conductual de los individuos, pueden ser incorporadas en los modelos epidemiológicos modernos[16].
Finalmente, desde una perspectiva epidemiológica, el factor distancia y la frecuencia de contactos físicos es un aspecto que deberá ser incorporado en los modelos matemáticos de precisión. Dichos enfoques estarán destinados a conocer la dinámica real de las enfermedades infectocontagiosas, con el fin de elaborar formas efectivas de intervención sanitaria, más cónsonas con el mundo real4. Nosotros, en nuestro afán meramente explicativo, marcamos el precedente de que la distancia (o frecuencia de contactos) es una variable que tiene una correlación negativa (o positiva) respecto a los factores y considerados en nuestro modelo.
Resultados
Deducción del número reproductivo básico
Notemos que un cálculo directo nos permite afirmar que el número reproductivo básico (casos secundarios generados por un primer infectado en una población libre de infección) está dado por:
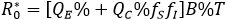
Expresión que cuando no existe diferencia conductual con consecuencias en la tasa de contagio (fS=fI=1), se reduce a R0=B%T . Como es sabido, corresponde al número reproductivo básico del clásico modelo susceptible - infeccioso - recuperado (QC = 0). Detalles de deducción de 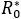 se pueden encontrar en la sección “elementos matemáticos”. De modo que la reducción porcentual i% en la cantidad de casos secundarios que produce un primer infectado en una población libre de enfermedad, debido a la existencia del grupo cuidadoso, es:
se pueden encontrar en la sección “elementos matemáticos”. De modo que la reducción porcentual i% en la cantidad de casos secundarios que produce un primer infectado en una población libre de enfermedad, debido a la existencia del grupo cuidadoso, es:
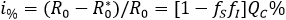
Se trata de un porcentaje que crece con una mayor representación del grupo cuidadoso o con el aumento de los niveles de cuidado, esto es, la disminución de los factores fS y fI. A modo de ejemplo, si una de cada 10 personas es capaz de reducir en un 50% sus encuentros infecciosos (como susceptibles o infecciosos), entonces la reducción porcentual en casos secundarios es de un 7,5%.
Advirtamos que si el grupo cuidadoso es absolutamente óptimo al bajar la tasa de infección, sea como susceptible o en rol de infeccioso (fS =0 o fI =0), tenemos que 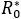 = (1 -QC%). Es decir, rebaja a lo más el número reproductivo en todo el porcentaje que representa en la población. En general, si
= (1 -QC%). Es decir, rebaja a lo más el número reproductivo en todo el porcentaje que representa en la población. En general, si 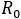 >1 , entonces
>1 , entonces 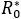 <1, si:
<1, si:
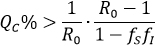
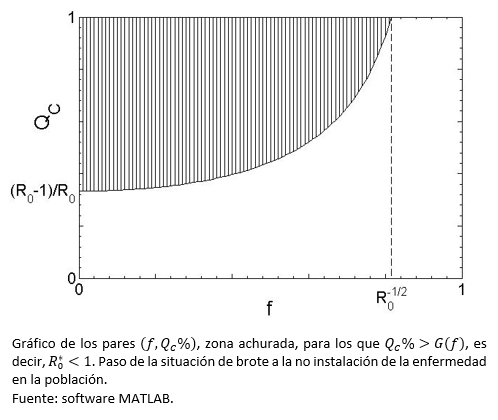
Al suponer fS=fI=f, entonces los pares (f,QC%) que logran bajar 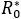 a menor que uno, son los tal que QC > G(f), con . Esto es, la zona achurada de la Figura 1.
a menor que uno, son los tal que QC > G(f), con . Esto es, la zona achurada de la Figura 1.
 Tamaño completo
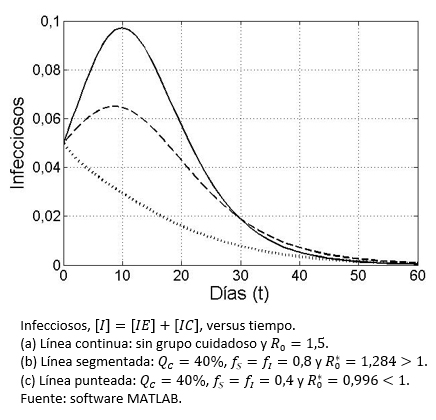
Tamaño completo La Figura 2 muestra tres escenarios para la evolución de los infecciosos en el tiempo, con grupo cuidadoso y sin él, en este último caso con 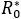 mayor o menor que uno.
mayor o menor que uno.
 Tamaño completo
Tamaño completo Relación prevalencia - tamaño grupo preventivo
La lectura de I% es importante en cuanto a casos secundarios menos, es decir, en la eliminación de algunas cadenas de propagación. Sin embargo, para conocer la prevalencia que es posible evitar, introducimos otros dos indicadores que pasan por realizar (simular) la dinámica de la infección.
Prevalencia evitada: denotaremos por [R]*(QC) la suma de los grupos de recuperados estándar y cuidadoso ([RE]+[RC]) tras “muchos” días del comienzo de la infección y paso del brote, suponiendo que la gente cuidadosa es un QC%. Así la prevalencia evitada como fracción de la que podría haber sido (sin la existencia del grupo cuidadoso) al final del brote, es:
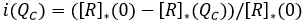
Se espera que este valor aumente con el tamaño del grupo cuidadoso, en términos marginales. Esto es, i'(QC)>0.
Prevalencia evitada per cápita: respecto a cuál es la prevalencia evitada por unidad porcentual, es decir en términos per cápita, el indicador es:
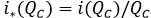 .
.
Notemos que se prueba que i* (QC) disminuye su valor con el tamaño del grupo cuidadoso. Esto es, el efecto de cada unidad porcentual es menor al crecer el grupo cuidadoso. En términos matemáticos se conjetura que i* (QC)<0.
Para efecto de simulaciones y gráficas, se considera que fS = fI = 0,1 y R0 = 1,2. Variamos el grupo cuidadoso en porcentajes que van entre el 2 y el 20%. Se corre el modelo con estos valores y luego se registran en la Tabla 4 los indicadores i(QC) y i*(QC).
 Tamaño completo
Tamaño completo 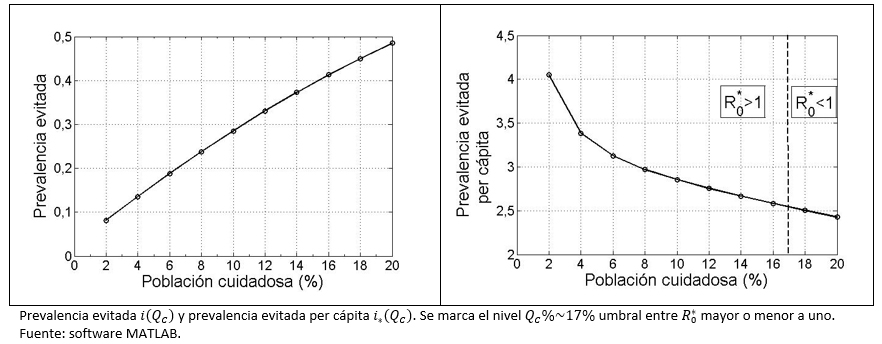 Tamaño completo
Tamaño completo Relación prevalencia - intensidad preventiva
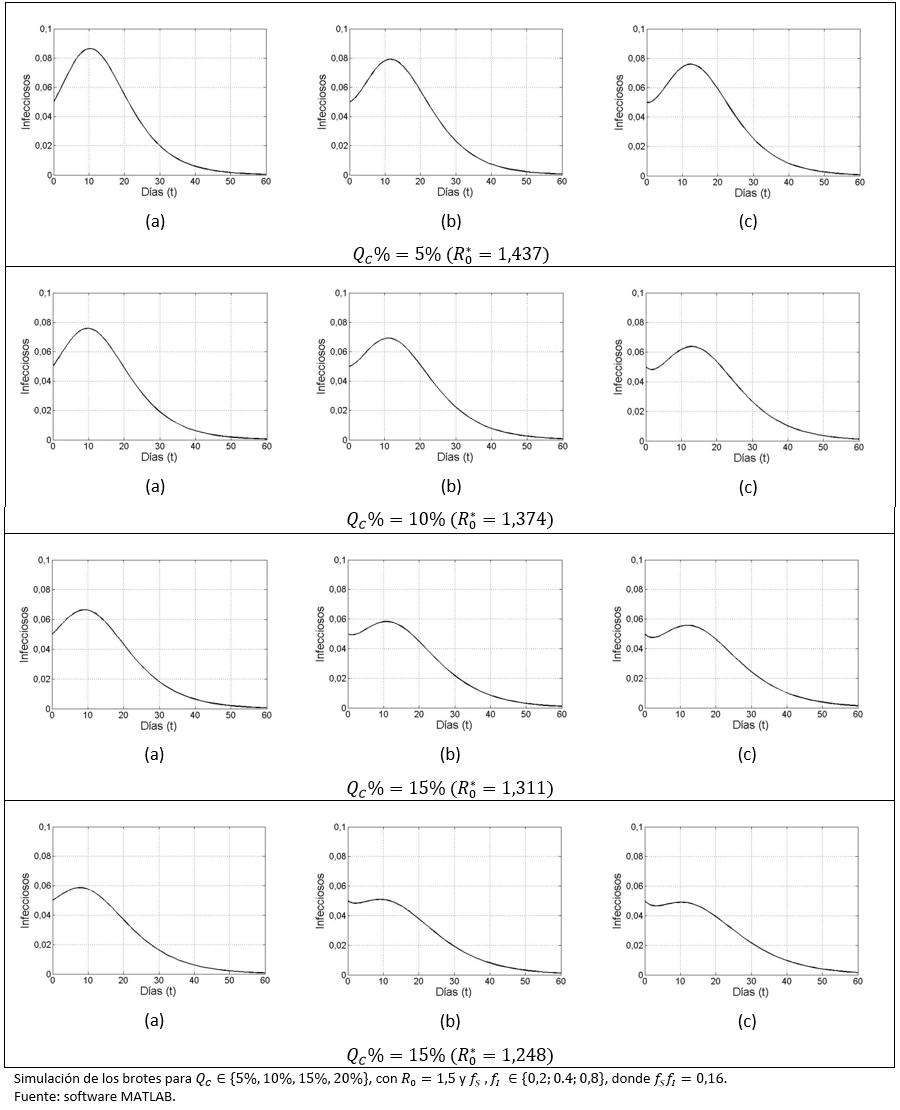
Entre los parámetros fS y fI una disminución en fI tiene más efecto en bajar el número de infectados que una en fS. Consideramos, para distintos QC% (5%, 10%, 15%,20%), los siguientes casos para el par (fS, fI):
(a) (0,2;0,8).
(b) (0,4;0,4) y
(c) (0,8; 0,2).
Como en todos los casos fSfI = 0,16, tenemos que 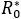 =(1-0,84QC%)
=(1-0,84QC%)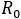 , con
, con 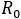 . Esto es, por cada valor de QC, en los tres casos (a-c) se mantiene el
. Esto es, por cada valor de QC, en los tres casos (a-c) se mantiene el 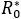 .
.
Aunque dado QC , 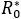 es el mismo en todos los casos (a-c), se observa que la prevalencia baja más para una disminución de que la misma en . Ahora, fijando (a), (b) o (c), al variar al alza, el tamaño del brote disminuye, como ya lo habíamos observado. Adviértase también el caso y (c), en que al principio (primeros días) el número de infectados tiende a la baja, pero siendo el número reproductivo básico mayor que uno luego hace un pulso suave.
es el mismo en todos los casos (a-c), se observa que la prevalencia baja más para una disminución de que la misma en . Ahora, fijando (a), (b) o (c), al variar al alza, el tamaño del brote disminuye, como ya lo habíamos observado. Adviértase también el caso y (c), en que al principio (primeros días) el número de infectados tiende a la baja, pero siendo el número reproductivo básico mayor que uno luego hace un pulso suave.
 Tamaño completo
Tamaño completo Discusión
Transformar el modo de vida (actividades vitales destinadas a satisfacer las necesidades grupales) de nuestras sociedades es una de las prioridades en salud pública[3]. Sin embargo, todo cambio debe partir desde el ser individual, esto es desde el estilo de vida propio (autorregulación para comprender mejor el entorno social y cultural al que pertenecemos). En este trabajo, a través de un modelo matemático de transmisión de una infección genérica, analizamos cuantitativamente el efecto epidemiológico de la existencia de grupos con conducta cuidadosa en salud. Los resultados demuestran que el grupo que aplica acciones preventivas para su propio cuidado y el de los demás, es un factor nada despreciable para la disminución del riesgo sanitario en la población total. De allí la importancia de dirigir acciones educativas desde las entidades sanitarias, con el fin de promover en las personas este tipo de conducta, tanto en cantidad como en calidad. Un estudio reciente, que usa la metodología del modelamiento matemático, incorpora la presencia de comportamientos humanos adaptativos destinados a reducir el riesgo de enfermedades infectocontagiosas[8].
Lograr articular una adecuada intervención social, orientada a mantener distanciamientos sociales (bajar la probabilidad de contacto contagioso) para reducir los riesgos de propagación de enfermedades infecciosas, sobre todo del estamento infeccioso, es el gran reto para la epidemiología moderna y la gestión en salud pública. Las poblaciones en general parecieran mostrar buena disposición a contribuir con las autoridades, siempre que exista convencimiento que ello repercute en un mejor estado de salud personal y general[2],[3], por lo que sumar argumentos científicos, en nuestro caso de base matemática, siempre será un aporte a la sociedad.
En este trabajo se analizó la dinámica epidemiológica a través de una estructura que cruzó estados respecto a la enfermedad (susceptible - infeccioso - recuperado) con una compartimentación conductual entre ciudadanos cuidadosos y ciudadanos estándar (distraídos) frente al riesgo. Esto, bajo el supuesto de que toda persona cuidadosa interactúa con el medio a través de factores (fS y fI ) de reducción de la tasa de contagio B%, según si su condición sea susceptible o infeccioso. En orden a comparar o medir variación en el potencial infeccioso, esencialmente se calculó el número de casos secundarios que produciría la llegada de un primer infectado, para dos casos con (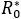 ) o sin (
) o sin (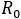 ) de grupo conductual cuidadoso. Así al suponer fS = fI = f, se detectan los pares (f, QC%) que logran bajar a un valor de no reemplazo de los infecciosos en la cadena de transmisión.
) de grupo conductual cuidadoso. Así al suponer fS = fI = f, se detectan los pares (f, QC%) que logran bajar a un valor de no reemplazo de los infecciosos en la cadena de transmisión.
En la práctica, lo anterior se podría lograr interviniendo a través de programas educativos sobre los parámetros sociales QC y f presentes en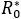 . Esto es, si hay condiciones para la propagación,
. Esto es, si hay condiciones para la propagación, 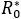 >1(zona no achurada en Figura 1), estas intervenciones deberían ser capaces en forma permanente de aumentar el tamaño del grupo cuidadoso y a la vez disminuir la probabilidad de contactos contagiosos (es decir, ir a la zona achurada de la gráfica). En general, según Fenichel y colaboradores[2], el implementar políticas públicas que motiven a la población para adquirir conciencia con respecto al distanciamiento epidemiológico interpersonal, es uno de los mayores retos para las autoridades en salud pública.
>1(zona no achurada en Figura 1), estas intervenciones deberían ser capaces en forma permanente de aumentar el tamaño del grupo cuidadoso y a la vez disminuir la probabilidad de contactos contagiosos (es decir, ir a la zona achurada de la gráfica). En general, según Fenichel y colaboradores[2], el implementar políticas públicas que motiven a la población para adquirir conciencia con respecto al distanciamiento epidemiológico interpersonal, es uno de los mayores retos para las autoridades en salud pública.
Conclusión
Para cuantificar la importancia del tamaño del tipo social cuidadoso, se definió un indicador de la prevalencia evitada (i(QC)). En este sentido, se observa un aumento de este indicador a medida que crece el tamaño del grupo cuidadoso. En contraste, un segundo indicador muestra que la prevalencia evitada per cápita (i*(QC)), produce un patrón contrario al anterior. Esto lleva a concluir que cada individuo cuidadoso, a menos número de conciudadanos del mismo tipo conductual, más contribuye en términos per cápita a evitar contagios futuros.
Finalmente, se exhiben evidencias bibliográficas que evidencian que para muchas enfermedades infectocontagiosas, la transmisión del agente patógeno ocurre en relación con la distancia que se mantiene de persona a persona en las relaciones sociales[4],[11]. Desde una perspectiva epidemiológica, el factor distancia y la frecuencia de contactos físicos es un aspecto que pudiera ser incorporado en los modelos matemáticos para introducir más realismo. Por ejemplo, en nuestro modelo los factores fS y fI permitirían elaborar en forma efectiva medidas de intervención sanitaria[4].
En la sección Ideas claves, reconocemos que lo generalista del modelo es una limitante, y que aspectos tales como estructura etaria, tipos de inmunidad, mecanismos de trasmisión, virulencia entre otros, no han sido incorporados. Sin embargo, estos aspectos merecen atención, aunque su incorporación en la modelización implica una mayor complejidad matemática e interpretativa que pudiera motivar nuevos estudios.
En relación con los objetivos propuestos, el modelo presentado es suficiente para entender el efecto general del grupo de comportamiento cuidadoso sobre la dinámica epidemiológica.
Elementos matemáticos
Ecuación diferencial modeladora
Se asume la población total igual a uno (normalización) para hacer las lecturas porcentualmente. Notemos que para cada X∈{E,C} tenemos [SX] + [IX] + RX] = QX% y además QE + QC = 1. La ecuación diferencial que modela el proceso es:
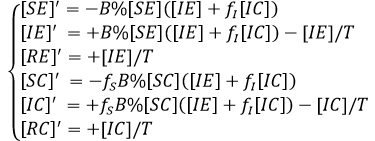
Si introducimos las variables [Y] definidas por [Y] = [YE] + [YC], Y∈{S,I,R} , tenemos:
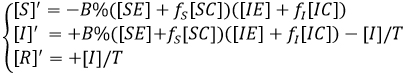
Este sistema se transforma en el modelo susceptible - infeccioso - recuperado de siempre cuando fS = fI = 1, el que es coherente para que el grupo cuidadoso no haga diferencia en la tasa de contagio.
Cálculo del número reproductivo básico
Para el cálculo del número reproductivo básico, se utilizaron las técnicas y notaciones propuestas por P. Van der Driessche y Watmough[17].
Se ordena el sistema[1] de modo que en las primeras ecuaciones aparezcan los grupos infecciosos, es decir, el vector de las variables del sistema con el nuevo orden queda:
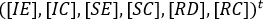
Donde significa trasposición.
El equilibrio libre de enfermedad está dado por X*= (0,0,QE%,QC%,0,0), y las matrices F y V-1 evaluadas en X* están dadas por:
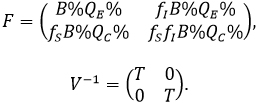
La matriz de la siguiente generación está dada por FV-1y se define el número reproductivo básico (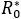 ) como el valor del radio espectral de dicha matriz. En donde tenemos que:
) como el valor del radio espectral de dicha matriz. En donde tenemos que:
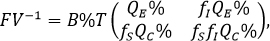
Notemos que el determinante de esta matriz es nulo y, por lo tanto, el valor propio dominante es:
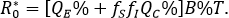
Notas
Roles y contribuciones de autoría
FCL: conceptualización, metodología, análisis formal, investigación, redacción (revisiones y ediciones), supervisión, administración del proyecto. MCH: conceptualización, investigación, redacción (revisiones y ediciones). JPGJ: metodología, investigación, gestión de datos, presentación de datos, preparación de manuscrito (desarrollo del borrador original), visualización.
Fuentes de financiamiento
Los autores declaran que no hubo fuentes de financiación externas.
Declaración de conflictos de interés
Los autores han completado el formulario de declaración de conflictos de intereses del ICMJE, y declaran no haber recibido financiamiento para la realización del reporte; no tener relaciones financieras con organizaciones que podrían tener intereses en el artículo publicado, en los últimos tres años; y no tener otras relaciones o actividades que podrían influir sobre el artículo publicado. Los formularios pueden ser solicitados contactando al autor responsable o a la dirección editorial de la Revista.
Agradecimientos
Agradecemos a la Línea de Análisis Epidemiológico del programa de Doctorado en Modelamiento Matemático Aplicado, Universidad Católica del Maule.

