Estadística aplicada a la investigación en salud
← vista completaPublicado el 1 de julio de 2011 | http://doi.org/10.5867/medwave.2011.07.5066
La prueba de la hipótesis
Testing the hypothesis
Resumen
En la sección Series, Medwave publica artículos relacionados con el desarrollo y discusión de herramientas metodológicas para la investigación clínica, la gestión en salud, la gesión de la calidad y otros temas de interés. En esta edición se presentan dos artículos que forman parte del programa de formación en Medicina Basada en Evidencias que se dicta por e-Campus de Medwave. El artículo siguiente pertenece a la Serie "Estadística Aplicada a la Investigación en Salud".
Introducción
Es frecuente, especialmente en el campo de la salud, que un profesional en ejercicio de su actividad se detenga en un fenómeno que lo hace pensar que el grupo al que está observando tiene un comportamiento especial respecto a una determinada variable.
Así, por ejemplo, un kinesiólogo puede pensar que los pacientes sometidos a una secuencia especial de ejercicios demoran menos en recuperar la función muscular que aquellos tratados con el método tradicional. A un médico psiquiatra radicado en Punta Arenas le puede parecer que los suicidios adolescentes son más frecuentes en su región. Un profesional de la nutrición puede creer que los pacientes con problemas de absorción intestinal responden mejor a una alimentación con verduras que con carnes. El director de salud de una municipalidad puede pensar que su consultorio tiene mejor resolución de problemas complejos que el consultorio del municipio vecino. Detrás de todas estas situaciones se esconde una hipótesis que espera para ser verificada.
Definición de hipótesis
Una hipótesis se define como una afirmación transitoria que debe ser sometida a prueba. La inferencia estadística propone un procedimiento para llevar a cabo la prueba de las hipótesis. Propone, primero, enunciarlas formalmente y luego contrastarlas con la evidencia de los datos. Son los datos, entonces, con su coro de características, los que dirán si una hipótesis es falsa o verdadera.
Este procedimiento se realiza considerando a los parámetros, que ya sabemos corresponden al universo, como los objetos para los cuales se enuncian las hipótesis. Dicho de otro modo, una hipótesis se enuncia para una característica del universo o población y se origina en la observación del comportamiento de la misma característica en un grupo restringido o muestra.
Una hipótesis por ejemplo, al decir: “estos enfermos demoran en promedio 25 días en recuperarse” está afirmando que, en el universo, el promedio de los pacientes tardan 25 días en mejorar. Será tarea del investigador probar la veracidad o falsedad de dicha afirmación contrastando el valor propuesto para el parámetro del universo (25 días), con los datos reales provenientes de una muestra cualquiera. Si luego de esta comparación resulta que el promedio obtenido en la muestra es de 22 días, se le encarga a la estadística que resuelva el dilema de si la diferencia entre el promedio muestral (22 días) y el poblacional (25 días) permite aceptar como verdadera la hipótesis planteada. Será el método estadístico el que permita en definitiva resolver este dilema, evaluando la significación de la diferencia entre 22 y 25.
¿Azar o no?
El método de las pruebas de hipótesis consiste fundamentalmente en establecer la probabilidad de que sea consecuencia del azar la diferencia existente entre dos cantidades. Se pueden distinguir dos situaciones:
a) Diferencia entre un valor muestral y un valor poblacional, o valor teórico.
b) Diferencia entre dos o más valores muestrales.
En el caso a se tratará de evaluar la diferencia entre un valor obtenido en la muestra (estadístico) y un valor correspondiente en el universo (parámetro), y en el caso b se evaluará la diferencia entre dos valores provenientes de dos muestras (estadísticos). Los valores que se comparen, ya sean de la muestra o del universo, pueden ser promedios, porcentajes u otros. Nosotros nos ocuparemos sólo de promedios y porcentajes.
En general, lo que hace una prueba estadística es evaluar la diferencia entre dos o más valores (dos promedios, dos porcentajes). Respecto de esta diferencia se elabora una hipótesis previa y se plantea formalmente en términos estadísticos.
Luego, usando la distribución de probabilidad adecuada, se calcula la probabilidad de la diferencia entre los valores comparados. Si la probabilidad de obtener tal diferencia es pequeña, diremos que dicha diferencia es significativa.
Una diferencia es significativa cuando la probabilidad de que se produzca por azar es pequeña.
Estadístico de prueba
Para realizar tan delicada operación debemos utilizar el instrumento apropiado: le llamaremos estadístico de prueba, el que podremos calcular con los datos de nuestra muestra. Luego buscaremos la probabilidad de ocurrencia del valor calculado en la tabla correspondiente (Normal, t de student u otra) y a la luz de la probabilidad obtenida tomaremos una decisión respecto de nuestra hipótesis.
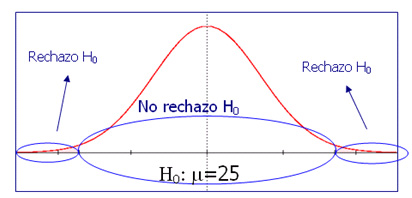
El esquema a seguir:
1. Plantear la hipótesis en términos estadísticos
Esta etapa consiste en representar el problema de investigación bajo la forma de dos hipótesis excluyentes: la Hipótesis Nula y la Hipótesis Alternativa.
- Hipótesis Nula. Esta hipótesis plantea que los valores comparados son iguales. Dependiendo del problema podrá presentarse como:
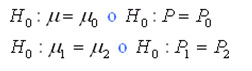
- Hipótesis Alternativa. Esta hipótesis plantea que los valores comparados son distintos y por lo tanto pertenecen a universos distintos. Dependiendo del problema podrá presentarse como:
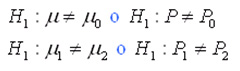
2. Elegir un nivel de significación
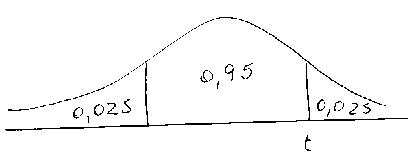
El nivel de significación es la probabilidad de que la diferencia observada se deba al azar. Interesa que esta probabilidad sea pequeña, por eso, en la práctica se utilizan valores iguales o inferiores a 0,05. El valor más usado es 0,05 pero también puede ser 0,04; 0,02; 0,01; etc. Al nivel de significación se le identifica con la letra griega alfa (α). Al elegir un valor de alfa concreto, estamos dejando la mitad de alfa en cada extremo de la distribución de probabilidades (α/2).
3. Calcular el estadístico de prueba a base de los datos muestrales
El estadístico que se utilice para la prueba de la hipótesis dependerá de los elementos que participan en él. Así, cuando se trate de comparar 2 promedios usaremos el estadístico t de student, cuando necesitemos comparar dos porcentajes muestrales usaremos Z, etc. Pero ya iremos viendo a cada uno de estos estadísticos actuar en terreno.
4. Buscar en la tabla correspondiente
Será necesario buscar a continuación:
- La probabilidad de obtener un valor igual o mayor al estadístico calculado, cuando éste sea positivo, o
- La probabilidad de obtener un valor menor o igual, cuando el estadístico sea negativo.
- En resumen: P(z > z0) cuando z0 sea positivo o P(z < z0) cuando z0 sea negativo.
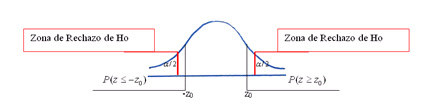
5. Comparar la probabilidad obtenida en la tabla con el nivel de significación elegido en el punto 2 y tomar una decisión respecto de las hipótesis planteadas
Parece evidente que para tomar una buena decisión es conveniente disponer de criterios. Debemos decidir si la hipótesis nula es verdadera o falsa. Entonces, de acuerdo a la evidencia aportada por los datos de la muestra aceptaremos o rechazaremos la hipótesis nula según el siguiente criterio:
Se rechazará la hipótesis nula si la probabilidad encontrada en la tabla es inferior a la mitad del nivel de significación(α/2).
6. Elaborar una conclusión derivada de la decisión
Una vez tomada la decisión sobre las hipótesis debemos exponer lo que esto significa en el contexto de nuestro problema particular.
7. Apoyar todo el proceso de análisis con un gráfico del problema
A la hora de tomar la decisión es muy útil y orientador un buen gráfico donde se consigne el nivel de significación, el valor del estadístico y la probabilidad asociada a él.
Nota: Con el objeto de facilitar la comprensión nos hemos limitado a tratar sólo las hipótesis bilaterales, ya que ésta es la forma más frecuente de plantear una hipótesis.

