Estadística aplicada a la investigación en salud
← vista completaPublicado el 1 de octubre de 2011 | http://doi.org/10.5867/medwave.2011.10.5195
Pruebas de hipótesis para comparar dos muestras
Hypothesis testing to compare two samples
Resumen
En la sección Series, Medwave publica artículos relacionados con el desarrollo y discusión de herramientas metodológicas para la investigación clínica, la gestión en salud, la gesión de la calidad y otros temas de interés. En esta edición se presentan dos artículos que forman parte del programa de formación en Medicina Basada en Evidencias que se dicta por e-Campus de Medwave. El artículo siguiente pertenece a la Serie "Estadística Aplicada a la Investigación en Salud".
Para desarrollar este tema seguiremos un esquema similar al del capítulo anterior. Estudiaremos tres situaciones problema que, sin ser las únicas, son las más frecuentes.
a) Comparación de la diferencia de promedios de dos muestras independientes.
b) Comparación de promedios de dos muestras pareadas.
c) Comparación de porcentajes de dos muestras.
Las preguntas
Antes de analizar la diferencia entre los promedios muestrales debemos responder algunas preguntas importantes que harán la diferencia en el procedimiento a seguir.
1. ¿Se trata de dos muestras independientes o pareadas?
Diremos que dos muestras son independientes cuando no se establece ninguna relación previa al análisis entre las unidades de una y otra muestra. Por ejemplo, sujetos de uno y otro curso, enfermos de dos consultorios, hombres comparados con mujeres.
En cambio diremos que se trata de muestras pareadas si en forma previa al análisis, se forman parejas entre los individuos de una muestra con los individuos de la otra muestra. Por ejemplo el caso con su control, distintas dietas pueden probarse en dos animales de la misma camada. Sin embargo, cuando queda más clara esta situación es cuando se comparan distintas medidas para los mismos individuos; por ejemplo, al medir antes y después del tratamiento a un mismo grupo de individuos se obtienen resultados pareados o correlacionados.
2. ¿Son conocidos los valores de la varianza, o las varianzas de los supuestos universos?
Como existe la posibilidad de que ambas muestras provengan de un mismo universo, entonces en ese caso se trataría de una sola varianza del universo. En ese caso hay que preguntarse ¿se conoce dicha varianza?
Pero también existe la posibilidad de que las muestras comparadas provengan de universos distintos y en ese caso habría dos varianzas universales. La pregunta en ese caso es ¿son conocidas las varianzas?
3. A la luz de las varianzas de las muestras, ¿podemos suponer que las varianzas son iguales?
Bueno, en esta parte y con todo derecho, podríamos reclamar en contra de las complicaciones de la estadística, pero seguramente el cumplimiento de estas exigencias nos permitirá obtener resultados más confiables.
Cada posible respuesta a estas interrogantes nos conducirá a ocupar una fórmula distinta para calcular el estadístico. Por ello veremos, en primer lugar, la forma de responder a las preguntas planteadas.
Las respuestas
La respuesta a la primera pregunta es fácil, porque se encuentra incorporada dentro del mismo problema de investigación: es una característica de los datos; forma parte del diseño de la investigación.
La segunda pregunta tampoco es tan complicada porque será cuestión de revisar los antecedentes de que dispone el investigador. Lo más frecuente es que este dato se desconozca y, por lo tanto, nosotros asumiremos que la o las varianzas del universo son desconocidas.
Para responder a la tercera pregunta se hace necesario realizar una prueba de hipótesis para probar la igualdad o diferencia de las varianzas. La realización de la misma no es difícil y es frecuente que los programas computacionales de análisis estadístico la hagan en forma automática sin que sea necesario solicitarla, y la entreguen como parte de los resultados. Como lo más frecuente es que las varianzas de las muestras comparadas tengan varianzas similares, nosotros haremos los análisis bajo este supuesto.
Hechas estas aclaraciones procederemos a describir en forma general los estadísticos que participan en cada situación.
a) Comparar los promedios de dos muestras independientes (con varianzas desconocidas y supuestas iguales)
Estadístico a utilizar: 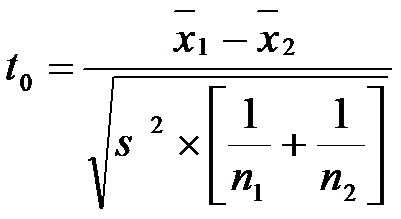
Donde:
1. “t0” tiene probabilidad de ocurrencia en la tabla de distribución t de Student con ![]() grados de libertad.
grados de libertad.
2. ![]() es la varianza común estimada.
es la varianza común estimada.
3. ![]() es el promedio de la muestra 1 y
es el promedio de la muestra 1 y ![]() es el promedio de la muestra 2.
es el promedio de la muestra 2.
4. n1 y n2 son los tamaños de las respectivas muestras.
b) Comparar los promedios de dos muestras pareadas
Estadístico a utilizar: ![]()
Donde:
1. “t0” tiene probabilidad de ocurrencia en la tabla de distribución t de Student con n-1 grados de libertad.
2. ![]() es la diferencia promedio entre las parejas de datos.
es la diferencia promedio entre las parejas de datos.
3. ![]() es la desviación estándar de las diferencias entre las parejas de datos.
es la desviación estándar de las diferencias entre las parejas de datos.
4. n es el tamaño de la muestra (número de parejas de datos).
c) Comparar los porcentajes de dos muestras
Estadístico a utilizar: 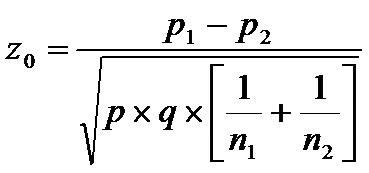
Con ![]()
Donde:
1. z0 tiene probabilidad de ocurrencia en la tabla de distribución normal.
2. p es la estimación del porcentaje común.
3. q es el complemento de p (100-p).
4. n1 y n2 son los tamaños de las respectivas muestras,

