Comments
← vista completaPublished on April 8, 2020 | http://doi.org/10.5867/medwave.2020.03.7874
Strengths and limitations of mathematical models in pandemics—the case of COVID-19 in Chile
Fortalezas y limitaciones de los modelos matemáticos en las pandemias: el caso de COVID-19 en Chile
Abstract
This short paper focuses on the role of mathematical models to analyze the impact of pandemics on health resources and the different trade-offs that may be included in them. There is a large body of literature suggesting that mathematical modeling may be helpful to estimate how much additional equipment and infrastructure are necessary to mitigate an increase in demand for health services during a large-scale outbreak of an infectious disease. I comment on the crucial role of these models with a special focus on their strengths and limitations.
Introduction
This paper is motivated by the current pandemic of coronavirus (COVID-19) around the world and particularly in Chile. A recent article by Gutiérrez-Aguilar et al. (2020)[1] addresses the critical problem of health resources available to face the novel coronavirus outbreak. This new coronavirus is related to the SARS-CoV with similar incubation and generation times, but with a lower rate of progression to severe disease and death given the appropriate medical support.[2] However, the human-to-human transmission of COVID-19 has shown to be highly efficient and now is present in over 200 countries and territories.[3],[4] The disease caused by this virus tends to be more severe in older adults and the chronically ill. A fraction of the people infected may need to be admitted to an intensive care unit (ICU) and require mechanical ventilation. This is the major problem affecting advanced countries as well as developing ones.[5] The reason is straightforward to understand. ICU beds and mechanical ventilators are limited, and their numbers in a given country are sufficient for the usual healthcare demand. We can say that most of the time, the limitation on ICU resources is not binding. However, for the COVID-19 outbreak, this is no longer true, and countries such as Italy have failed to provide this intensive care with the consequence of increasing their death rate.[6] All this makes it essential to have mathematical models to forecast the demand for ICU resources correctly. In this article, I discuss the elements to consider performing this task successfully.
Small versus large models
Mathematical models can be used to estimate different types of variables and differ in their methodology. What variable or what model is used will depend upon the question to be answered. For example, we could use a model to estimate the number of infected people based on an assumption about the basic reproduction number (R0) or we could use data on infected people to estimate R0. If the disease has known behavior, then some parameters can be assumed as known. However, if the disease is new—as the COVID-19 case—then we must deal with all the problems associated with estimating such parameters. A critical parameter value to know is R0 and this can be a function of variables with different parameter values. Thus, depending on the environmental setting R0 is going to be different. In mathematical terms,
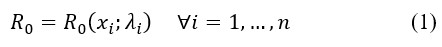
Equation (1) shows that the basic reproduction number depends upon a set of variables and there is a parameter λi related to each variable xi. Therefore, if we want to estimate R0, then we need to know what variables should be included. Assuming we know the right model specification, then we need to estimate the parameters λi. In this stage, we could encounter two main issues: (i) measurement errors in the data, and (ii) self-selection of individuals in the database. Both problems can be addressed in statistical terms, but gathering new information is necessary to make the corrections. All this is analyzed in a static setup. That is, time is not playing a role so far. However, as the variables, xi, evolved over time, t, then R0 will change as well. This can be represented as,
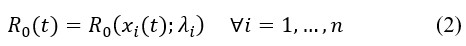
Equation (2) implies that the basic reproduction number can evolve over time as the variables do so, even if we assume time homogeneity for the coefficient parameters λi. Hence, the exercise of estimating R0 is not trivial.
The estimation of any parameter to input in a mathematical model is beset with the same level of complexity. How simple or complicated these estimations are, will depend upon the availability of data and/or the knowledge about the phenomenon itself.
The previous discussion is directed to highlight the importance of understanding the nature of the parameters entering into a model that is used to predict or forecast a given variable or a set of them. What parameters need to be known depends upon the underlying assumptions of the model. Usually, as the level of complexity increases, so does the number of parameters to be known. Greater complexity in the model is often associated with some gains in representing reality at the cost of needing more information (knowing more parameters)[7]. Whether the model should be large or small depends upon the situation. We need to consider that using a large model with unprecise parameter values could cause more harm than good, which leads me to the next section.
All models are wrong, but some are useful
The title of this section is attributed to the statistician George Box, who expressed the idea that a model, even complex, is a simplification of reality. Nonetheless, some models can be very helpful in understanding a phenomenon, or to forecast a variable. Economists have had to tackle the problem of building useful and applicable models for over a century. In Turnovsky (2011)[8] we find a piece of advice provided by Nobel Laureate Robert Solow on how to do successful and useful models, summarized by the following three ideas:
- Make it simple.
- Do it right.
- Make it plausible.
Underlying this suggestion is the idea that models should have the just right level of complexity, meaning that models should not be simpler than necessary, but also not more complex than needed. Achieving this balance is, of course, very complicated. However, a rigorous analysis of the problem being addressed should shed light on the assumption to be made and the parameter values that are available. The paper by Córdova-Lepe et al. (2020) is a good example of this. They build a model making several assumptions that are plausible and use a model that is simple enough to be tractable and complex enough to provide helpful insight. That is the just right level of complexity.
COVID-19 and the collapse of the healthcare system
Continuing with the discussion of the Córdova-Lepe et al. (2020) paper, they study the minimum daily effort such that the healthcare system may not collapse during the COVID-19 outbreak. In their model, assumptions are clearly stated, and sensitivity analysis is performed to analyze the overall impact of the different parameters. They acknowledge that a parameter that needs to be estimated is the daily effort to reduce contagion. Nonetheless, small changes of this parameter are quite relevant. With aid of numerical simulations, they achieve this qualitative finding. Stating dates for the collapse of the healthcare system without observing precise parameter values for the COVID-19 phenomenon is nearly impossible at this stage, even with a simple model that requires little information. Small models like this one can be extremely helpful to highlight that some actions are crucial, and at the same time, small differences can make a huge difference. Specifically, they find that to curb the epidemic of this respiratory disease, small actions such as isolation and social distancing could make the difference between the healthcare system collapsing or not.[9] They also point out that these measures may have undesirable economic impacts, which is not modeled in their paper because it is not their focus. It goes without saying that the economy is a relevant aspect for policymakers.[10]
Concluding remarks
Understanding the limitations of models is critical to provide helpful information to decision-makers and the general public. When studying mathematical models, more effort should be put into understanding the impact of the underlying assumptions on the results or predictions. Similarly, a more considerable effort should be exerted in analyzing the sensitivity of the model to different parameter values. Furthermore, the numeric ranges chosen should be transparently justified providing all available sources. The criteria above are recommended standards to improve the credibility of our analyses by other modelers, planners, and policymakers. Once a large-scale outbreak of an infectious disease happens, there is not much time to build models or estimate parameters. Therefore, having contingency plans based on different scenarios and models is vital to overcome a health crisis successfully.

