Methodological notes
← vista completaPublished on April 7, 2021 | http://doi.org/10.5867/medwave.2021.03.8149
Minimal clinically important difference: The basics
Diferencia mínima clínicamente importante: conceptos básicos
Abstract
This article is part of a collaborative methodological series of narrative reviews on biostatistics and clinical epidemiology. This review aims to present basic concepts about the minimal clinically important difference and its use in the field of clinical research and evidence synthesis. The minimal clinically important difference is defined as the smallest difference in score in any domain or outcome of interest that patients can perceive as beneficial. It is a useful concept in several aspects since it links the magnitude of change with treatment decisions in clinical practice and emphasizes the primacy of the patient’s perception, affected by endless variables such as time, place, and current state of health, all of which can cause significant variability in results.
Main messages
- The minimal clinically important difference is defined as the smallest difference in score in any domain or outcome of interest that patients can perceive as beneficial or harmful.
- It links the magnitude of change to treatment decisions in clinical practice and emphasizes the primacy of patient’s perception.
- It is a tool when planning the design of scientific studies and the calculation of the sample size.
- It is a variable concept, and there can be multiple estimates for a health situation. Not all methods of estimating the Minimal clinically important difference result in universally comparable or useful values.
- This article explores and summarizes in a friendly language the basic concepts related to the minimal clinically important difference, traced in articles published in the main databases and specialized reference texts, oriented to the training of undergraduate and graduate students.
Introduction
Usually, both clinical practice and medical research involve evaluating changes in different outcomes or various health conditions such as pain, functionality, satisfaction with treatments, quality of life, among others [1]. One of the challenges resulting from these evaluations is determining if the differences represent a statistically significant change and, if so, whether this constitutes a really important clinical benefit or detriment for patients [2].
Most studies are limited to quantifying the size of the differences in health conditions and their significance in statistical terms, based on conventional hypothesis tests (such as the Student's t-test or the Chi-square test), which depend largely on the number of people evaluated [1]. However, patient-reported outcomes (PROMs) are increasingly common to incorporate both their perspective and the impact that the disease and the treatments generate [3]. PROMs would be defined as any report that comes directly from patients about how they function and how they feel in relation to a health condition and its therapy [4]. However, another tool is patient-reported experience measures (PREMs). This would be defined as a measure of a patient's perception of his/her personal experience in the medical care he/she has received [5]. However, the human perception of most health conditions is subjective and individual and is affected by a myriad of variables (time, place, and current health state) that can cause great variability in results [1] and generates a new challenge in the standardization of evaluations, their interpretations, and their comparisons. Due to this variability, there is not necessarily a single clinical difference considered important for each outcome, but rather a range of estimates considered clinically significant, depending on the population and its characteristics.
This article is part of a methodological series of narrative reviews about general biostatistics and clinical epidemiology topics, which explore and summarize published articles available in the main databases and specialized reference texts in a friendly language. The series is aimed at the training of undergraduate and graduate students. It is carried out by the Chair of Evidence-Based Medicine of the Escuela de Medicina de la Universidad de Valparaíso, Chile, in collaboration with the Research Department of the Instituto Universitario Hospital Italiano de Buenos Aires, Argentina, and the Centro de Evidencia Universidad Católica. This article aims to present basic concepts about the minimal clinically important difference (MCID) and its use in the field of clinical research and evidence synthesis.
What is the 'minimal clinically important difference'?
MCID is defined as the smallest difference in score in any domain or outcome that patients can perceive as beneficial or harmful and that it would require – in the absence of troublesome side effects and high costs – a change in the management of patient health care [6]. Therefore, the MCID is an aid tool when planning the design of scientific studies and the calculation of the sample size [6].
Example: visual analog scale
The MCID is used in continuous outcomes where the measurement of a certain scale or score value is allowed, and it varies according to the definition of the scale to be used (there is no universal scale). An example is the visual analog scale (VAS), which is a pain measurement scale whose range varies between 0 and 100 mm, in which it is understood that a difference of approximately 20 mm (difference of means) between two measurements at different times has a relevant clinical outcome for people with pain > 70 mm [7]. So, when evaluating a patient with headache who reports that at the beginning of the symptoms it had an intensity on the pain scale of 80/100, and after a few minutes, it indicates that the pain decreased to an intensity of 70/100, everything would indicate that it is not a clinically relevant result. However, if in the second intensity measurement, this patient reported a score of 60/100, this result would seem to be more important than if it had decreased only by 10 mm on the scale. Thus, in research that seeks to demonstrate the usefulness of a specific intervention to treat headache, it would be expected that the intensity of the headache that patients present would decrease by at least 20 mm on a pain scale. If, in a study, drug X is compared with placebo, and the mean pain in the group that received drug X is 40/100 and in the group that received placebo is 60/100, then it could be said that this score difference is clinically relevant. There was a 20-mm decrease in the pain scale in the patients who received the intervention compared to those who received a placebo.
The MCID in acute pain can vary widely between studies and may be influenced by baseline pain, definitions of improvement, and study design. In fact, the MCID is context-specific and potentially misleading if it is improperly determined, applied, or interpreted [7].
Methods to establish the minimal clinically important difference
Mainly, there are two methods for estimating the minimally important difference as follows:
- The anchor-based method
- The distribution-based method
1) Anchor-based method
The anchor-based methods allow a comparison between a patient's situation reflected by an outcome measure (i.e., the result of the measurement on an outcome) and an external criterion. This external criterion is nothing more than the perception of the patient himself. This method then compares the changes between scores with an anchor question. For example, use the question: "do you feel better after intervention X?" as a reference to determine if the patient improved after treatment compared to baseline, based on the patient's own experience. A global pain rating scale (“much worse”, “somewhat worse”, “almost the same”, “somewhat better”, and “much better”) could be used in this case to understand the patient's impression of change. The anchor question needs to be easily understandable and relevant to patients. Typical anchors may be ratings around a change in health status, presence of symptoms, disease severity, response to treatment, or prognosis of future events such as death or job loss [8].
Continuing with the example, when asked, "do you feel better after intervention X?" Those responses that refer to a change "somewhat better" or "much better" are considered of special interest since they inform the researcher of a clinical improvement that patients have verified from their own subjectivity. The next point to take into account would be the changes (averages) of the score in the instrument used for each answer to the anchor question in order to establish the points of interest (e.g., minimum difference for improvement or minimum difference for deterioration), often considered as the thresholds that account for the smallest change that correlates with clinical improvement (Table 1).
 Full size
Full size Another method based on the anchor used to set the MCID is the observation of a sample of patients at a given point in time. These are grouped into categories according to the external criteria used. For example, if the pain variable is still taken into account ("I have no pain", "I have moderate pain", and "I have extreme pain"), the difference between two contiguous groups on the scale should be observed (e.g., "moderate pain" and “I don't have pain”) and identify the mean scores of the instrument of interest in these groups. Thus, the difference between the mean score of the groups "I have moderate pain" and "I have no pain" would be the MCID [9].
2) Distribution-based method
The distribution-based methods attempt to estimate how likely a difference is to be significant beyond chance from the spread (variance) of the data. In other words, they do not involve the experts’ opinion or patients’ evaluations. They are based on the statistical properties of the result of a certain study [10].
Because distribution-based methods are not derived from individual patient’s assessments, they probably should not be used to determine the MCID. Its logic is based on statistical reasoning, where it can only identify a minimum detectable effect, that is, an effect which is unlikely to be attributable to random measurement error. The lack of an “anchor” linking these numerical scores to assessing what is important to patients means that these methods fail to identify important and clinically meaningful outcomes for patients, as they do not include their perspective. In fact, the term MCID is sometimes replaced by "minimal detectable change" when distribution-based methods calculate the difference. For this reason, these methods are not recommended as the first line for the determination of an MCID [11].
This method has the advantage of simplicity because it does not require an external criterion. However, it produces similar results for both worsening and improvement, making interpretation more straightforward but more questionable, as a higher MCID is often observed for worsening rather than improvement [12].
This approach involves standard deviation fractions, the effect size, and the standard error of the mean as estimates for calculating the MCID. Standard deviation is a measure used to quantify the amount of variation or spread in a set of data values. There seems to be a universally applied rule of thumb that the MCID is equal to 0.5 standard deviations. Cohen and Hedge's formulation of effect size are the most widely accepted reference parameters: 0.2 standard deviations for "small" effect sizes (or what we compare to MCID), 0.5 standard deviations for “moderate” effect sizes, and 0.8 standard deviations for “large” effect sizes [1]. This criterion is reported in 90% of the studies that use distribution-based methods. Despite the simplicity and widespread use of this approach in identifying MCID, no clear distinction is made between improvement and impairment of an intervention.
Health-related quality of life measures are important factor in making rational decisions about treatment options. Identifying significant health-related changes in quality of life reflects an emerging emphasis on the assessment of meaningful outcomes for patients. An example of this would be subjecting a group of cancer patients to the Functional Assessment of Cancer Therapy scale at two different times: at the start of therapy and in a second follow-up stage; and thus be able to evaluate four dimensions of health-related quality of life as follows:
- social well-being,
- family well-being,
- emotional well-being, and
- functional well-being.
If the statistical difference detected between these two moments were less than 0.5 standard deviations, it would indicate that it is not a significant change. However, if this result exceeded that value, it would be the minimum detectable change [13].
Limitations in establishing the minimal clinically important difference
MCID is a variable concept, and there can be multiple estimates for the same outcome or health status. Not all methods of estimating the MCID result in universally comparable or useful values [14]. Anchor-based methods have been criticized for their variability, which depends on multiple factors such as the time between evaluations (which could favor recall bias), the direction of the change to define if it is benefit or deterioration, the type of anchor question used (secondary outcome or global evaluation score), the perspective to be considered (patients, relatives, caregivers, professionals, funders, among others), the demographic characteristics of the study population (age, socioeconomic level, and education), stability symptoms, the severity of the disease, or the type of intervention received [1],[14]. Methods based on distribution have been questioned due to the lack of assessment of the “importance” of the change and for using mathematical analyses of the distribution of the study population with some inconsistencies [14].
So, the term “clinical relevance” does not seem to be easy to define and quantify. Who decides what is clinically relevant, the patient and/or the healthcare professional? And how do different views on "clinical relevance" vary between patients? As an example, in a situation where we present two patients (A and B), both bedridden due to Guillain-Barré syndrome. If patient A is an elderly patient, he/she could consider “being able to walk with assistance” as a clinically relevant improvement. And if patient B is a young adult, he/she might consider “being able to compete in professional sports again” as a clinically relevant change. Both are affected by the same disease. However, they have a different interpretation of the term “clinical relevance” and would have different goals for their treatment [9].
An instrument has been proposed to assess the credibility of MCID estimates based on anchoring methods. In this study, five items are taken into account that should be fulfilled to give high credibility to the measurement, namely:
- The patient or their caregiver must respond directly to both the outcome measure reported by the patient and the anchor.
- The anchor question must be understandable and relevant to the patient.
- The anchor must show a good correlation with the measure reported by the patient.
- The MCID must be accurate.
- The analytical method must ensure that the difference or threshold for the MCID makes a small but important difference [8].
Limitations on use of the minimal clinically important difference
MCID varies not only by patients and the clinical context being studied but also by the method used to estimate it, each with specific underlying assumptions that affect the value and precision of the final result. That is why it should not be blindly applied or universally accepted. It is necessary to consider whether the population in which the MCID is to be applied is similar to the population in which it was estimated, considering the diagnosis and the expectations of improvement of each population. Furthermore, applying the MCID may have different implications if groups of patients or individual patients are considered when determining the effectiveness of the interventions [15].
Implications for GRADE
The GRADE (Grading of Recommendations Assessment, Development and Evaluation) approach offers a transparent and structured process to develop and present summaries of evidence reflecting the degree of certainty surrounding the estimates of the effect of the interventions [16]. The certainty of the evidence is established by assessing five domains, namely: risk of bias, inconsistency, indirect evidence, imprecision, and publication bias. It is often used to communicate the findings of systematic reviews to patients, health professionals, and the general public as clearly and simply as possible, using standardized statements or statements with controlled language that have been translated into many languages.
The GRADE methodology is also used in other types of documents that report the results of systematic reviews, such as clinical practice guidelines or health technology assessments [17]. In the framework of systematic reviews, the MCID can be used as a threshold for evaluating the precision of the measures of effect of the interventions, mainly when they are about outcomes reported by patients evaluated on continuous scales.
The MCID can be understood in this case as the minimum difference to be detected, which allows calculating the size of the sample required to find this difference in clinical studies and, in turn, evaluating whether the studies complied with that sample size (a concept known as the “optimal information size” or OIS). If the OIS is achieved, an estimate of the effect of an intervention can be considered accurate if its 95% confidence interval (95% CI) does not overlap with the MCID value, since it would imply that the analyzed intervention can generate relevant clinical changes in the outcome of interest.
However, the researchers in charge of the systematic reviews could lower the certainty rating of the evidence related to the outcome of interest by one level if the OIS is achieved and the summary estimate of the effect overlaps with the MCID, which implies that the evaluated intervention could generate both relevant clinical changes and changes not noticeable by the patients [18].
From a clinical point of view, the precision of the effect of a given intervention could be evaluated from the evaluation of the 95% CI and the clinical significance of the result. This indicates in what range the result could oscillate 95% of the cases if an experiment were carried out 100 times. It gives us an idea of the possibilities that we could find. Therefore, the wider the range, the lower the confidence of the evaluated intervention [18].
To consider that the effect of an intervention is imprecise, the confidence interval of the estimator and the number of events or subjects included in the sample must be assessed. Thus, if a clinical decision or recommendation changes depending on whether one extreme of the 95% CI is taken into account, our confidence in the estimate of the effect should decrease. Likewise, even with a precise 95% CI, if the number of episodes or subjects evaluated is low, the need to reduce the quality of the evidence should be considered. Returning to the example of patients with headaches, where the pain scale decreased by two points in the intervention group compared with the control group, the 95% CI should be evaluated. In this case, a 95% CI with a range between −3 and 1 and taking into account that a difference of two points would indicate a clinically significant result, it would result in two different scenarios: that the true value is a decrease of three points that would be interpreted as a clinically important difference, or that the difference between both groups was only one point so that the value would no longer be important (Figure 1).
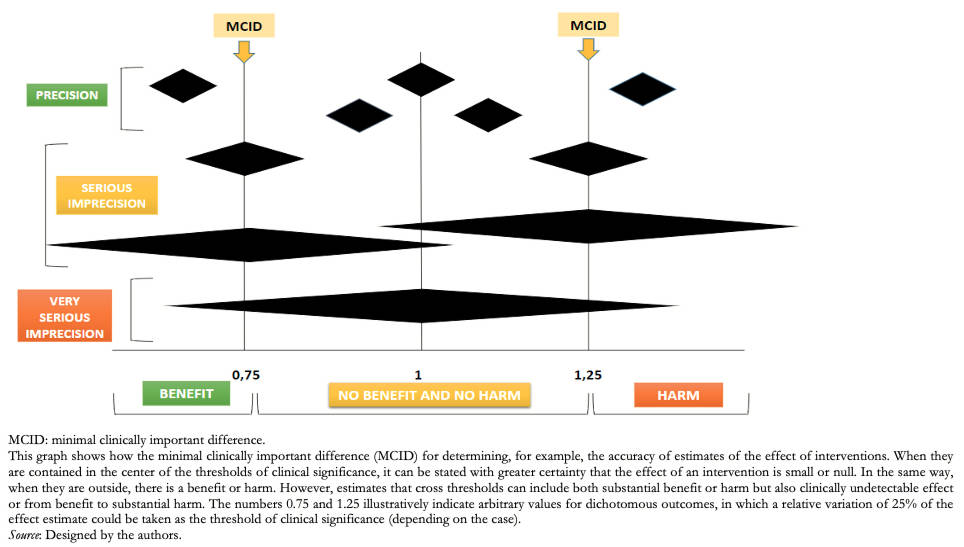 Full size
Full size Relative importance of outcomes
Decisions related to health care require considering the effect of the interventions and their importance for the patients, but they must also consider the relative importance of the outcomes on which the interventions act [19], including the values and preferences of patients. This implies that in the face of two interventions with similar effect sizes that reach the MCID, the inclination for one or the other intervention will depend on the relative importance that patients assign to each outcome [19]. For example, if intervention “A” has shown a clinically important effect on the 6-minute walk test in patients with chronic obstructive pulmonary disease and intervention “B” also demonstrated clinically important effects on the perceived sensation of dyspnea, the choice of treatment would be in favor of intervention “B” if the values and preferences of the patients consider dyspnea as a more important outcome than the distance walked.
Considerations for dichotomous outcomes
Establishing a threshold to determine whether the effects produced by the interventions are considered trivial, small, moderate, or large in terms of dichotomous outcomes can be difficult and, to a greater or lesser extent, depends on the relative importance that patients place on the outcome of interest. Therefore, it is necessary to partially contextualize the importance of the outcome of interest and establish thresholds in absolute terms [16]. This way, if the 95% CI of the effect size overlaps with the null effect (relative association measure of 1 or absolute association measure of 0), it could be concluded that:
- The evidence is imprecise, and we cannot answer in a specific way, reliable in relation to the effect of the intervention.
- The evidence is accurate, and the intervention is, in fact, ineffective, or the effect size is trivial.
To determine the second option, the 95% CI must be narrow enough and not include the established threshold. If included, the effect of the intervention can be considered null or trivial. If not included, the effect size could be considered significant [16].
It is necessary to consider both the probability of the outcome and its relative importance to determine the threshold. By way of illustration, if we estimate an absolute reduction in the incidence of an event from 12% to 9% (absolute difference of 3% and relative difference of 25%), this may be trivial if it is minor bleeding that does not require hospitalization, but it may be important when it comes to mortality. Conversely, a 60% to 30% reduction in the incidence of minor bleeding (30% absolute difference and 50% relative difference) may become relevant for decision-making. Often, however, a relative reduction of 25% is taken as a guide number (“rule of thumb”) as a minimum relevant difference [18]. However, as we saw in the previous examples, this minimum reduction depends on the absolute risk and the relative importance of each outcome [20].
Conclusions
The changes in the different health conditions routinely evaluated in clinical practice and research need to be interpreted beyond their statistical significance. The MCID incorporates and emphasizes patient perspectives concerning treatments and their health status and links them in decision-making.
There are various methods for determining the MCID; however, anchor-based methods are the most frequently used. Furthermore, the MCID constitutes a variable concept from which multiple estimates can be found for the same outcome or health status.
The MCID has important implications when assessing the certainty of the evidence, both in the framework of systematic reviews and in decision-making.

