Review article
← vista completaPublished on September 28, 2022 | http://doi.org/10.5867/medwave.2022.08.2552
Analysis of SEIR-type models used at the beginning of COVID-19 pandemic reported in high-impact journals
Análisis de modelos tipo SEIR utilizados en los inicios de la pandemia COVID-19 reportados en revistas de alto impacto
Abstract
Introduction The Susceptible-Exposed-Infected-Recovered (SEIR) mathematical-epidemiological model has been exhaustively used since de beggining of the COVID-19 pandemic. These models intended to predict hospital burden and evaluate health measures to contain its spread. In this sense, flaws have been evidenced in the predictions of the first published models. It is considered necessary to evaluate the differences in the approach and verification of the models.
Objectives We carried out a systematic review of the articles published in journals indexed in the Web of Science, of the first quartile and with an impact factor greater than two, that met the selection and inclusion criteria following the PRISMA-ScR standards. We included a total of 32 articles, which were evaluated according to demographic characteristics such as the month of receipt and publication, the country of origin of the information, the subject matter of the journal, and the characteristics of the modeling such as the presence of additional compartments, graphical analysis, conceptual model approach, interpretation of the basic reproductive number, and estimation of parameters.
Methods Articles published in medical and health journals were predominant from February to July 2020. These articles most frequently used data from China and mostly focused on SEIR or full quarantine compartment models. The articles published in journals in mathematics were predominant from August to December 2020. Models used data from different world regions, considering a greater diversity of compartments such as asymptomatic patients or partial or complete quarantine.
Results The articles analyzed mostly use SEIR-type models expanded with additional compartments. There are discrepancies in the breadth and methodological quality of the articles published according to the journal’s subject matter. The unification of quality criteria for describing the models in any journal is recommended.
Conclusions The articles analyzed mostly use SEIR-type models expanded with additional compartments. There are discrepancies in the breadth and methodological quality of the articles published according to the journal’s subject matter. The unification of quality criteria for describing the models in any journal is recommended.
Main messages
- The Susceptible-Exposed-Infected-Recovered (SEIR) model approach is widely used to represent pandemic phenomena and their evolution.
- Mathematical models have had successes and failures during the COVID-19 pandemic.
- This paper provides tools for decision makers to determine which models have relevant information and are appropriate for particular situations.
Introduction
Throughout history, infectious diseases have immensely impacted the population’s morbidity and mortality. Multiple studies on projections of the behavior of epidemics have been known for centuries [1]. Currently, increased access to mobility leads to a rapid spread of epidemics [2,3]. COVID-19 is an infectious pandemic caused by the SARS-CoV-2 pathogen, first detected during the 2019 epidemic in Wuhan, China, which was reported as an emerging pneumonic coronavirus disease with high morbidity and mortality rates [4,5]. Unlike other epidemics with a shortage of investigators, many scientists are now studying this pandemic globally and regionally. In this regard, the Susceptible-Exposed-Infected-Recovered (SEIR) model approach is widely used to represent this epidemiologic phenomenon [1,3].
This work aimed to categorize scientific publications from high-impact journals that proposed SEIR-type models to predict the COVID-19 pandemic spread in its early stages when oi was challenging to obtaining reliable sources on the risk of COVID-19 disease. Moreover, essential elements in the analysis of the models were evaluated. These elements included the quality of the modeling and the parameters that compose them to provide tools for decision-makers and determine which published models have relevant information and are appropriate to their particular situation.
First epidemic models
The first mathematical models related to infectious diseases were carried out in 1761 by D'Alambert, who developed a method to analyze the competing risks of death [6] and in 1766 by Daniel Bernoulli, studying the age-specific equilibrium prevalence analysis of individuals who were immune to chickenpox [7]. Approximating the number of contagions through mathematical expressions has a long history, motivated by infectious outbreaks that prompted its appearance. These were the cases of John Snow in 1855 in a Cholera outbreak and Daniel Bernoulli in 1760 in a smallpox outbreak [6]. Then, Pyotr Dimitrievich En'ko published the epidemic model in 1889, studying successive measles outbreaks of previous decades [8].
At the beginning of the 20th century, the physician and mathematician Anderson G. McKendrick considered that the probability of a new person suffering from a contagious infection is directly proportional to the number of susceptible and infected people at an instant [9]. This reasoning took on a more general approach, leading him to publish the system of differential equations in 1927, together with the biochemist and mathematician William O. Kermack. Decades later, this model would be the basis of the Susceptible-Infected-Recovered (SIR) model [10], which would be the protagonist of the modeling of several epidemics in the following decades [11]. However, unsolved problems and mathematical curiosity motivated changes to the SIR model. Thus, the Susceptible-Exposed-Infected-Recovered (SEIR) model was born [1,9], which subdivides the total size of the human population at time t, denoted as N(t), into susceptible S(t), exposed E(t), infected I(t) and recovered R(t). Therefore, for the human population we have: N(t)=S(t)+E(t)+I(t)+R(t).
Advantages of SEIR models
As the disease spreads, the susceptible individual S(t) moves first to the exposed population E(t) [10], and considering an incubation period in between, the exposed individual moves to the infectious population I(t). After ending the disease, the infectious individuals move to the recovered population R(t), where the deceased individuals are also represented. This model recognizes the biological existence of incubation time in infectious diseases, allowing a more realistic approach [11,12]. Adding more realistic elements to the mathematical model requires more parameters and assumptions. Unfortunately, in many real-world circumstances, reliable data are unavailable to perform the required parameter quantifications, resulting in model predictions with considerable error. Therefore, model results should be treated with caution.
Although many mathematical models cannot make accurate predictions, mainly due to a lack of data, they are handy for estimating the effect of control measures even before the start of the epidemic [1,9]. Through these models, it is also possible to predict thresholds in the density of infected individuals above which an epidemic is triggered, final values of the number of individuals that will be affected by the disease, the influence of external or seasonal factors, and, in some cases, the spatial spread of epidemics [1,3]. In addition, SEIR-type models help forecast a disease’s evolution, obtain estimates of its characteristics (such as mortality and hospitalization rates), and know the impact of interventions to predict the evolution of COVID-19.
Each compartment represents a group of individuals in the same health state, e.g., susceptible or infectious. The connections between the compartments indicate the direction and rate of passage from one health state to another. It should be emphasized that there is no natural birth and mortality due to the short coverage time of the model and its incidence of mass action [1,3,9].
Limitations of SEIR models
Since the first Susceptible-Infected-Recovered (SIR) model was published for the initial SARS-CoV-2 outbreak in Wuhan (China) [12], at least 18 papers describing the behavior of the epidemic through SIR or SEIR-type models had already been published by April 2020. For example, by February 20, 2020, Zhan C et al. published as a preprint one of the first Susceptible-Exposed-Infected-Recovered (SEIR) models based on parameters fitted with data on the spread of the virus in 367 cities in China [13].
An essential aspect of SEIR models is assessing an intervention’s impact. However, it is difficult to consider all possible interactions between interventions in the same model and find parameters close to reality through simulations [1,3,9]. Moreover, these models do not involve the variability of the sources of the information nor the possible errors and biases. In this way, two parameters from different contexts could be used in the same model. Mathematical models have had hits and misses during the COVID-19 pandemic. For example, at the beginning of the pandemic and after the first cases of infection in the United Kingdom, several mathematical models were published, some of which postulated the possibility of a more benign outcome by overestimating the idea of the protective effect of rapid herd immunity [14,15].
Methods
Systematic reviews used in the epidemiological context are frequently applied to clinical trials or observational studies to summarize, through a meta-analysis, the estimates made for comparable populations [12]. Heterogeneity among the populations included in the review may introduce biases in the overall estimate obtained after condensing the results.
On the other hand, a systematic review of mathematical models does not intend to collect studies measuring the same set of variables in comparable populations. They aim to collect modeling works under the same set of assumptions (in our case, underlying SEIR-type models) with parameters that characterize an epidemic at different times and places by the same infectious agent and host.
Frequency tables were used in this work to compare modeling approaches that successfully represent the population’s data distribution characteristics and, therefore, predict their sample realizations. However, statistical comparison of mathematical models is only possible when two or more different models seek to predict data from the same population. When the same modeling strategy (in our case Susceptible-Exposed-Infected-Recovered) is applied to predict different populations, even if they are similar in terms of the infectious agent, comparisons are not possible. Consequently, this review aims to measure differences in approaching Susceptible-Exposed-Infected-Recovered (SEIR) models. The choice and evaluation of data sources and processes of verification of adequacy were analyzed. Likewise, as the source of information regarding each model comes from published articles, we establish to what extent the reading of the article allows us to evaluate each model with the information provided.
Search strategy and identification
In this review, an advanced search for publications was performed through the Web of Science (WoS) integrated online scientific information service provided by Clarivate Analytics, between May 21, 2020, and April 30, 2021, according to the Preferred Reporting Items for Systematic Reviews and Meta-Analyses for Scoping Reviews (PRISMA-ScR).
The search terms for titles and abstracts by subarea in medicine or mathematics used were: ALL= (covid* OR SARS* OR coronavirus*) AND ALL= (model* OR SEIR OR math*) AND PY= (2020) AND IS= (Issn OR Issn), where ISSN corresponds to the journals according to subject category. Additionally, the journals' first quartile (Q1) ranking for 2019 and impact factors greater than or equal to two were considered (See Figure 1). There were no restrictions on languages, publishers, countries of publication, or types of documents.
Articles inclusion flowchart.
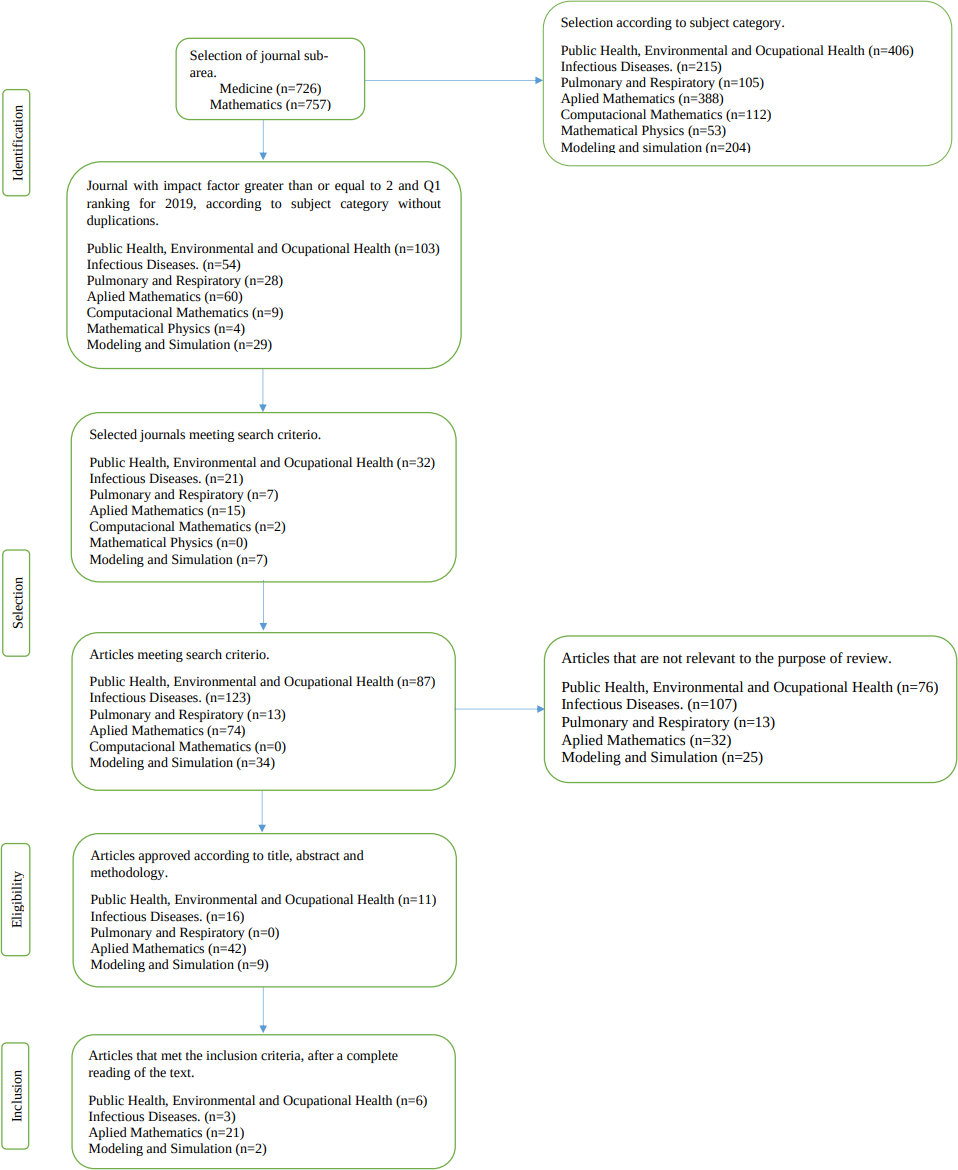
Selection and eligibility of studies
The tabulation of records was performed in Microsoft Excel, proceeding to the elimination of duplications and initial review of the title and abstract. Three of our authors extracted the information independently in order to avoid errors. The records of potentially eligible articles were reviewed independently by three of our authors to confirm their relevance. Any discrepancies were resolved by mutual agreement.
Inclusion criteria
Studies had to meet the following predetermined criteria for inclusion:
-
Does the basic structure contain a population SEIR-type mathematical model?
-
Does it study the dynamics of people with SARS-CoV-2 infection?
-
Is the methodology based on mathematical modeling of these dynamics?
Exclusion criteria
Studies were excluded if they did not provide information to measure differences in the mathematical modeling approach. Letters to the editor, case reports, review articles, and news reports were also excluded. Articles in which the full text was not available were also excluded.
Data extraction
The following information was extracted from the articles selected from the SEIR-type models related to COVID-19 and published on the dates defined in the search strategy, as well as from those selected and included in this analysis: first author, journal name, the month of publication, subject category, and reference (Table 1). Three of our authors extracted the data independently to avoid errors in this process.
Assessment of included articles
Three of our authors independently performed quality assessments of the articles to ensure their relevance to our objective, according to the following checklist:
-
Do they propose compartments for the population additional to those corresponding to the classical SEIR model?
-
Is the mathematical modeling based on a conceptual model suitable for COVID-19?
-
Does it include graphical analysis?
-
Is the location and time-period for which the study was conducted documented?
-
Is the basic reproductive number (R0) found and interpreted?
-
Are the values of the parameters considered and their sources of information presented?
Two authors independently verified the information obtained to avoid errors in its inclusion. Differences were resolved by mutual agreement.
Data analysis
The variables were recategorized to delimit the description of the results. The following regions were defined: China, Asia (comprising all Asian countries except China), North America (the United States and Canada), Europe, Latin America, Africa, Oceania, and combined (when the information used came from sources in different regions).
The study months were grouped into February to July 2020 and August to December 2020, as shown in Table 2. The subareas of medical and mathematical journals correspond to the following subject categories classified by the Web of Science as public health, environmental and occupational health (Med.PHEOH), infectious disease (Med.ID), pulmonary and respiratory (Med.PR), applied mathematics (Mat.A), computational mathematics (Mat.CM), mathematical physics (Mat.MP), and modeling and simulation (Mat.MaS). The information collected in each of the phases was tabulated using spreadsheets. Absolute and relative frequencies were extracted for each category, and corresponding contingency tables were made (tables 1–3).
Results
Study inclusion characteristics
The identification, selection, eligibility, and inclusion process is shown in Figure 1. We selected 331 articles for COVID-19 analysis through SEIR-type models that met the search criteria. The title, abstract, and methodology were read, and 78 articles were selected to read the full text and review the inclusion criteria. Thus, a total of 32 articles were obtained for subsequent evaluation, excluding articles that did not meet these criteria. All articles were retrospective. Those with insufficient information based on the inclusion criteria were excluded. The characteristics of the included articles are summarized in Table 1 and Figure 2.
Compartment details of SEIR-type models of included items.
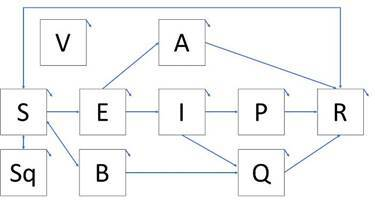
Source: Prepared by the authors of this study.
Figure 2 shows a conceptual model representing the main compartmental findings of the articles included in this review, as shown below:
-
Susceptible (S), exposed (E), infected (I), and recovered (R) compartments were shared in all articles and represented the classic SEIR model.
-
Three articles included an Sq compartment corresponding to individuals who temporarily cease to be susceptible due to quarantine. One of these articles also included a B compartment corresponding to suspected cases of infection, which were subsequently confirmed to be in full quarantine or returned to susceptibility.
-
Compartment E traditionally involves infected but non-infectious people. However, in 13 articles, this compartment had an infecting character, although more limited than compartment I.
-
Compartment A was evident in nine articles and consisted of asymptomatic infected people, usually with lower infectivity, except in one article where the infectivity was similar to compartment I.
-
Compartments P and Q mentioned partial quarantine (with low infectivity) or complete quarantine (no infectivity). Of the 15 articles that included quarantined compartments, seven involved hospitalized people.
-
Compartment R included those recovered, while deaths in the different articles occurred in any of the compartments, being more frequent in I, P, and Q.
-
Three articles included the possibility of reinfection of recovered persons.
-
Two articles considered vaccinated people, representing individuals moving from susceptible to recovered populations. No articles were found that considered reinfection of vaccinated people.
-
Compartment V referred to reservoirs. Two articles dealt with the virus’s presence in the environment, while three others represented the virus in the Wuhan seafood market.
Descriptive analysis
Table 3a and b describe the absolute and relative frequencies by row for the thematic categories, region, and general models.
shows 14 (44%) articles on mathematical models based on data from China. Of these, 64% were published from February to July and 36% from August to December. It is worth noting that, of the nine articles published in medical and health journals, 89% used data from China, in contrast to 26% from mathematical journals. [c2] [c3] Table 3
Table 3b shows that 12 included articles corresponded to classic Susceptible-Exposed-Infected-Recovered (SEIR) models, with no asymptomatic or quarantine compartment. However, in four of these, the E compartment had individuals who were partially infecting. Within the Susceptible-Exposed-Infected-Asymptomatic-Partial Quarantine-Infected-Recovered (SEAIR) models, we found five articles, three of which included reservoirs. In Susceptible-Exposed-Infected-Partial Quarantine-Recovered (SEIPR) models, there were two with partially infecting E compartments. In Susceptible-Exposed-Infected-Complete Quarantine-Recovered (SEIQR) models, nine articles were located, five of which had partially infecting E compartments. Only one article involved a Susceptible-Exposed-Infected-Partial Quarantine-Complete Quarantine-Recovered (SEIPQR) model, which included a viral reservoir. Finally, two articles were Susceptible-Exposed-Asymptomatic-Infected-Complete Quarantine-Recovered (SEAIQR), and one was Susceptible-Exposed-Asymptomatic-Infected-Partial Quarantine-Complete Quarantine-Recovered (SEAIPQR).
There are relevant differences between the model classes and subject categories of the journals in which the articles were published. Articles published in journals in the mathematical area included a greater diversity of model extensions. In contrast, there was a greater tendency to use Susceptible-Exposed-Infected-Recovered (SEIR) and Susceptible-Exposed-Infected-Complete Quarantine-Recovered (SEIQR) models in the medical and health areas. Table 2 summarizes the months of article submission and publication according to subject categories. The date of reception of an article from the medical and health area was unavailable. All articles included in the medical and health journals were submitted before July, while this percentage decreased to 70% for the journals in the mathematical area. A similar pattern was observed with the publication dates, where 67% of the articles were published in the first seven months for the medical and health area, compared to 35% in the mathematical area.
Concerning the evaluation criteria, 100% of the included articles used a graphical analysis of cases to evaluate the SEIR-type model. However, while all the articles published in mathematical journals described the sources of information for parameter estimation, only 67% of those published in medical and health journals met this criterion. In both types of journals, the use and interpretation of the basic reproductive number were found in approximately 70% of cases. Finally, a conceptual, theoretical model approach was described in 78% of medical and health journal articles, while this percentage decreased to 52% in mathematical journals.
Discussion
This paper presents the variations in the categorization of scientific publications according to diverse approaches to compartmental models. These models have been widely used to study the behavior of infectious diseases in the last three decades [1,2,3,6]. The Susceptible-Infected-Recovered (SIR) models are suited to different scenarios, assuming that individuals, once infected, can start infecting other individuals [10,11]. In contrast, Susceptible-Exposed-Infected-Recovered (SEIR) models include "latent infections" in the exposed compartment (E). This model considers individuals exposed to contagion and whose ability to infect other individuals has not yet developed but eventually will move to the infectious compartment (I) [1,9].
The exposed compartment (E) represents the existence of latent infection periods, i.e., incubation periods, which are usually pre-symptomatic and described in most infections affecting humans [10,11,12]. This approach allows a more realistic representation of the contagion dynamics of SEIR models. Although some models had an exposed compartment, some articles were excluded since they did not meet the definition of such a compartment.
We found that 40.6% of the included articles contemplated the possibility of infectivity to persons represented in the exposed compartment (E), even if this was low. Interestingly, of the 32 articles based on the SEIR model, only eight (25%) of these consisted of a classical SEIR model, with no additional compartments and no partial infectivity in the exposed compartment.
Data reported by different studies showed that both asymptomatic and symptomatic infected persons spread SARS-CoV-2 to susceptible individuals once they are in contact [28,30,41,45]. Thus, it is possible to establish transmission in two ways: from person to person and from the environment to the person [48,49,50].
The measures implemented to prevent the spread of COVID-19 mean that once infected persons sneeze or cough, the virus spreads in the environment [4,51]. In addition, terminating restrictions imposed on international travel around the world led to an increase in the transmission of COVID-19 [5,51]. SARS-CoV-2 survives in the environment for a few days, so this would increase the probability of contagion for susceptible individuals in contact with such an environment. This is especially noticeable in the first days of the COVID-19 outbreak, even before biosecurity and hygiene protocols were applied [4,19,52].
Conclusions
The SEIR-type mathematical-epidemiological model has been employed in several published articles based on available information to predict pandemic behavior. Initially, the data used came from China and other Asian countries affected early, which allowed them to obtain the first estimates of the contagion rate, latency time, and infectious time, thus improving the predictions' quality. Most of the first articles were published in medical and health journals, although later articles published in mathematical journals predominated. It should be noted that most of the available graphical analysis descriptions come from articles published in mathematical journals, even though the methodological approach to the same problem is similar.
The differences in editorial requirements, as well as the training and experience of the peers, may have influenced the fact that articles in the medical and health journals more often have a conceptual model, usually broader and more detailed. Meanwhile, journals in the mathematical area usually describe the stability and validation of the model. In addition, articles published in the mathematical area also use extensions of the Susceptible-Exposed-Infected-Recovered (SEIR) model more frequently.
Finally, it is recommended to establish more general guidelines to ensure quality in the description of modeling in an article related to the mathematical modeling of epidemics, in particular with SEIR-type models. This measure would improve comparability between the different results. It is also encouraged to use appendices for publications to expand the analysis if required.

