Estadística aplicada a la investigación en salud
← vista completaPublicado el 1 de junio de 2011 | http://doi.org/10.5867/medwave.2011.06.5053
Estimación de parámetros
Parameter estimation
Resumen
En la sección Series, Medwave publica artículos relacionados con el desarrollo y discusión de herramientas metodológicas para la investigación clínica, la gestión en salud, la gesión de la calidad y otros temas de interés. En esta edición se presentan dos artículos que forman parte del programa de formación en Medicina Basada en Evidencias que se dicta por e-Campus de Medwave. El artículo siguiente pertenece a la Serie "Estadística Aplicada a la Investigación en Salud".
Definiciones
El campo de la inferencia estadística trata básicamente de predicciones y generalizaciones. Por ejemplo, se puede afirmar, basándose en opiniones recogidas por medio de una encuesta, que en las próximas elecciones presidenciales el candidato de gobierno obtendrá 60% de los votos. Para hacer esta afirmación fue necesario determinar el porcentaje de votos favorables en una muestra seleccionada de la población. Al porcentaje obtenido de esta forma se le llama “estadístico” o “estadígrafo”.
A partir de este valor se puede estimar el porcentaje real de votos que dicho candidato obtendrá el día de la elección. Este porcentaje real proviene del universo de votantes o población y se le llama parámetro. En general, cualquiera de las medidas de resumen -promedio, desviación estándar, porcentaje, tasa- se considera “estadístico” si proviene de la muestra, y “parámetro” si proviene del universo o población.
La inferencia estadística entrega las herramientas para realizar afirmaciones acerca de un parámetro de la población, basándose en el valor del respectivo estadístico proveniente de una muestra. Para realizar estas inferencias es necesario conocer, previamente, la distribución de probabilidad del estadístico. A la distribución de probabilidad de un estadístico se le llama “distribución muestral”.
Podemos tomar una muestra, calcular en ella un estadístico (promedio o porcentaje, por ejemplo) y luego hacer afirmaciones respecto del correspondiente parámetro. Esto se conoce con el nombre de estimación de parámetros, y se puede hacer de dos formas:
- Estimación puntual: consiste en asumir que el parámetro tiene el mismo valor que el estadístico en la muestra.
- Estimación por intervalos: se asigna al parámetro un conjunto de posibles valores que están comprendidos en un intervalo asociado a una cierta probabilidad de ocurrencia. También se llaman “intervalos de confianza” debido a que la probabilidad asociada a ellos es la confianza de los mismos. Así, diremos que un intervalo de 99% de confianza es más confiable que uno de 95%. También se define la confianza de la estimación como la probabilidad de acertar con el intervalo.
La estimación que tiene valor estadístico para promedio o media y para el porcentaje de la población es esta última, que explicaremos a continuación.
Estimación de la media de la población
Explicaremos este punto con el siguiente ejemplo: queremos estimar el número de hijos promedio que tienen las mujeres de una población determinada. Con este objeto se seleccionó, por muestreo aleatorio simple, una muestra de 20 mujeres a quienes se entrevistó, obteniendo como resultado un promedio de 3,2 hijos y una desviación estándar de 0,8. Con estos resultados podríamos hacer una estimación puntual y decir que la población de interés tiene en promedio 3,2 hijos. Pero esta estimación tiene el inconveniente de que se desconoce el error que se está cometiendo.
Si a esta estimación le asignamos un error, que llamaremos E, podríamos decir que el promedio de hijos de la población está ubicado dentro de un intervalo de estimación que tiene como límite inferior 3,2 - E y como límite superior 3,2 + E. De este modo, le asignamos al resultado un intervalo de estimación. Si además le damos a este intervalo una probabilidad de ocurrencia de los valores comprendidos en él, habremos construido un intervalo de confianza para el promedio de hijos de nuestra población de mujeres.
Entonces, generalizando lo que se explicó para la variable “promedio de hijos”, podemos decir que:
Un intervalo de confianza para estimar el promedio de la población está constituido por los siguientes elementos: el promedio de la muestra y el error de estimación.
El elemento esencial en la construcción del intervalo de estimación es el error.
¿Cómo se obtiene el error en la construcción de un intervalo para el promedio?
Desarrollando la fórmula siguiente:
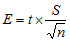 |
Está compuesta por la desviación estándar de la muestra (S), el tamaño de la muestra (n) y, aquí aparece un elemento nuevo, t –Student-, que corresponde a una distribución de probabilidad muy similar a la distribución normal.
En la tabla de t los valores se buscan en función de dos cosas:
- la probabilidad que hemos elegido para nuestro intervalo, y
- los “grados de libertad” que se calculan restando 1 al tamaño de la muestra (n).
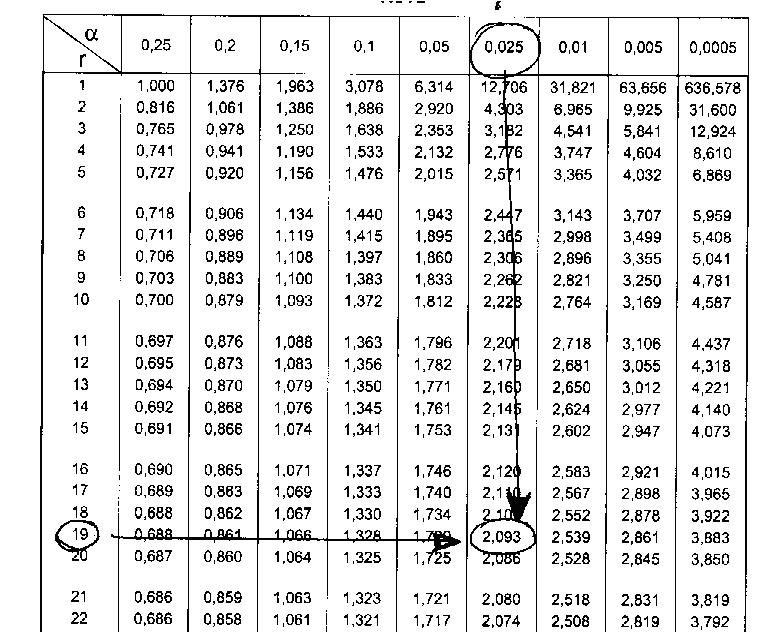
En nuestro ejemplo elegimos una confianza de 95% que, asociada a los 19 grados de libertad (n-1), nos conduce a un valor de tabla t de Student igual a 2,093. Ya veremos en forma detallada el uso práctico de la tabla t, recordemos por ahora el valor de “t” encontrado porque lo utilizaremos para la construcción del intervalo.
Volviendo a la fórmula para calcular el error, vemos entonces que el error está compuesto por tres elementos:
- El valor t que se obtiene de la tabla t de Student.
- La desviación estándar de la muestra.
- El tamaño de la muestra.
Volviendo a nuestro ejemplo, calculemos el error. Recordemos que deseamos conocer el número promedio de hijos que tienen las mujeres en esa población y que, estudiando una muestra de 20 mujeres, el resultado fue un promedio de 3,2 hijos y una desviación estándar de 0,8.
¿Cuáles son, entonces, los elementos que nos permitirán calcular el error de nuestra estimación?
| El valor t que obtuvimos de la tabla t de Student | t = 2,093 |
| La desviación estándar de la muestra | S = 0,8 |
| El tamaño de la muestra | n = 20 |
Reemplazando esos valores en la fórmula obtendremos el error, que es:
| |
Intervalo de estimación
Construiremos ahora el intervalo de estimación, sumando y restando al promedio, el error. De esta manera el límite inferior será: promedio - E; y el límite superior: promedio + E.
Límite inferior (a) = 3,2 - 0,37 = 2,83
Límite superior (b) = 3,2 + 0,37 = 3,57
De este modo se consigue un intervalo (2,83; 3,57) que nos permite estimar, con 95% de confianza, que el promedio de hijos en la población de mujeres está entre 2,83 y 3,57.
En resumen, los pasos en la construcción de un intervalo de confianza para la estimación del promedio son:
- Obtener una muestra aleatoria.
- Calcular promedio y desviación estándar muestral.
- Elegir la confianza del intervalo (95% ó 99%).
- Obtener el valor de t en tabla.
- Calcular el error de estimación.
- Calcular los límites del intervalo (a y b).
De estos 6 puntos, ya hemos tratado los puntos 1, 2, 5 y 6.
Sólo haremos un comentario sobre el punto 3: la elección de la confianza. Lo decide el investigador y se podría elegir cualquier valor, pero por lo general se usa 95% ó 99%. La elección de uno u otro dependerá de la confianza y la precisión que necesitemos para nuestra estimación, ya que si el intervalo es más grande, la precisión será menor; por lo tanto, un intervalo de 99% tiene mayor confianza y menor precisión que uno de 95%.
Cómo buscar un valor en la Tabla t de Student
El primer paso es calcular los grados de libertad (gl) restando 1 al tamaño de la muestra: gl = n-1
El segundo paso es elegir la confianza del intervalo. Elijamos un 95%.
Tercero, buscar el valor de t. Como la distribución es simétrica, un intervalo de 95% (0,95) al centro de la curva deja necesariamente 2,5% (0,025) en cada extremo de la curva. El valor que buscamos deja sobre sí a 2,5% de los sujetos, ó 0,025 si trabajamos sobre base 1, que es como están los valores en las tablas (véase gráfico).
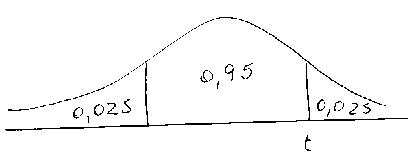 |
En la primera fila de la tabla aparece el símbolo alfa, que indica la probabilidad, debemos buscar allí un t con alfa 0,025. De allí hacia abajo, en toda la columna, se encuentran los valores de t asociados a 0,025 de probabilidad. Luego buscamos en la primera columna los grados de libertad (n-1). En el cruce de la fila de los grados de libertad con la columna de la probabilidad está el valor de t que nos interesa.
En nuestro ejemplo el tamaño de muestra es de 20 sujetos, por lo tanto tenemos 19 grados de libertad. Entonces buscaremos en la tabla un valor de t para 0,025 de probabilidad y con 19 grados de libertad. Encontramos t = 2,093.
 |

