Estadística aplicada a la investigación en salud
← vista completaPublicado el 1 de septiembre de 2011 | http://doi.org/10.5867/medwave.2011.09.5136
Comparación del porcentaje de una muestra con el porcentaje del universo
Comparison of the percentage of a sample with the percentage of the universe
Resumen
En la sección Series, Medwave publica artículos relacionados con el desarrollo y discusión de herramientas metodológicas para la investigación clínica, la gestión en salud, la gesión de la calidad y otros temas de interés. En esta edición se presentan dos artículos que forman parte del programa de formación en Medicina Basada en Evidencias que se dicta por e-Campus de Medwave. El artículo siguiente pertenece a la Serie "Estadística Aplicada a la Investigación en Salud".
En la comparación del porcentaje de una muestra con el porcentaje del universo, el problema para el investigador se explica con el siguiente ejemplo: en una población determinada, un 28,2% de las personas presentan algún problema de salud mental. Producto de su experiencia en un consultorio rural, un profesional de la salud sospecha que en la población asignada a ese consultorio el porcentaje de personas con problemas de salud mental es superior al de la población. Con el objeto de probar su hipótesis toma una muestra al azar de 63 personas, encontrando 31% de ellas con problemas de salud mental.
A la luz de estos antecedentes, ¿se puede aceptar la hipótesis de que el porcentaje de problemas de salud mental en este consultorio es distinto de 28,2?
¿Cuáles son los datos que entrega el problema?
| P0=28,2 | Porcentaje del universo con problemas de salud mental |
| Q0=71,8 | Porcentaje del universo sin problemas de salud mental |
| p0=31 | Porcentaje de la muestra |
| n=63 | Tamaño de la muestra |
1. Las hipótesis serán:
H0 : P=28,2
H1 : P≠28,2
2. Elegiremos un nivel de significación: α = 0,04
3. El estadístico de prueba será:
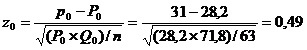
4. Buscamos en la tabla normal la probabilidad asociada a un valor de z mayor de 0,49.
Como la tabla entrega la probabilidad de encontrar un valor de z inferior a 0,49 (0,6879), la probabilidad de valores de z mayores a 0,49 se obtiene por diferencia: 1-0,6879=0,3121.
Comparamos la probabilidad encontrada con la mitad del nivel de significación: α / 2 = 0,02
5. Dado que el valor de z calculado (0,49) se encuentra más o menos al centro de la curva, su probabilidad según tabla es de 0,3121; que resulta mayor a la mitad del nivel de significación elegido (α / 2 = 0,02).
Esto nos conduce a la decisión de aceptar la hipótesis nula (ver gráfico).
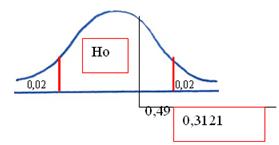
6. Aceptar la hipótesis nula significa aceptar que el porcentaje de problemas de salud mental en la muestra no es significativamente distinto del porcentaje del universo.
Por lo tanto, el porcentaje de problemas de salud mental del consultorio estudiado no es distinto al de la población.

