Estadística aplicada a la investigación en salud
← vista completaPublicado el 1 de noviembre de 2011 | http://doi.org/10.5867/medwave.2011.11.5254
Comparación de los promedios de dos muestras independientes (con varianzas desconocidas pero supuestas iguales)
Comparison of the averages of two independent samples (with variances unknown but assumed equal)
Resumen
En este artículo se discute y se ejemplifica cómo evaluar la comparación de los promedios de dos muestras independientes (con varianzas desconocidas pero supuestas iguales), cómo realizar comparación de dos muestras con observaciones pareadas, y cómo realizar comparación de los porcentajes de dos muestras. Mediante situaciones hipotéticas y con datos simulados, se demuestran paso a paso los procedimientos para evaluar estas situaciones.
Comparación de los promedios de dos muestras independientes (con varianzas desconocidas pero supuestas iguales)
El problema para el investigador es el siguiente: en una maternidad de la Región Metropolitana se sospecha que los hijos de madres adolescentes tienen un peso de nacimiento diferente, probablemente menor, al peso de los recién nacidos de madres mayores de 25 años.
Con el objeto de probar la hipótesis se tomó una muestra de 36 recién nacidos de madres adolescentes obteniendo un promedio de peso al nacimiento de 2,85 kg, con una desviación estándar de 0,5 kg, y una muestra de 28 recién nacidos de madres mayores de 25 años obteniendo en promedio 3,05 kg y una desviación estándar de 0,42.
Identifiquemos los elementos del problema.
- Promedios de las muestras 1 y 2
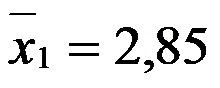 y
y 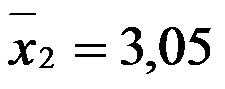
- Desviaciones estándar de las muestras 1 y 2
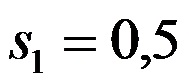 y
y 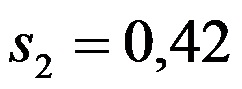
- Tamaños de las muestras n1=36 y n2=28
Una vez identificados los datos del problema, buscaremos la solución guiados por el esquema básico que usted ya conoce del capítulo anterior.
1. Planteamiento de hipótesis en términos estadísticos
![]()
Esta hipótesis (hipótesis nula) plantea que las muestras, aunque tienen promedios diferentes, provienen de un mismo universo y que la diferencia observada se debe al azar.
![]()
Esta hipótesis (hipótesis alternativa) plantea que las muestras provienen de universos con promedios distintos.
2. Elegimos un nivel de significación
![]()
Calcular el estadístico de prueba:
![]()
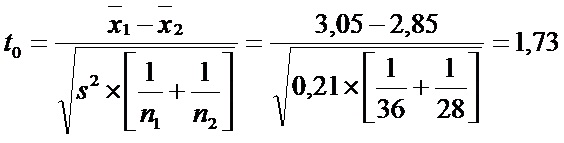
Nota: Se aconseja restar al mayor de los promedios, el menor, de tal modo que la diferencia resulte positiva y facilite así su búsqueda en la tabla. Entonces el estadístico de prueba es t=1,73
3. Como los grados de libertad son 62 (n1 +n2-2), buscamos en la tabla “t”, con 60 grados de libertad, la probabilidad de ocurrencia que tiene un valor de “t” igual o superior a 1,73
Vemos en la tabla que 1,73 se encuentra entre 1,671 y 2,000 por lo tanto la probabilidad de un valor superior a él es mayor que la mitad de alfa (0,025) (probabilidad de la cola).
Queremos conocer la probabilidad de encontrar un valor de “t” mayor a 1,73 para compararlo con 0,025 (la mitad de alfa).
Según la tabla, la probabilidad de valores de “t” mayores a 1,671 es 0,05 y la probabilidad de valores de “t” mayores a 2,000 es 0,025, entonces la probabilidad de valores de “t” mayores a 1,73 estará entre 0,05 y 0,025, esto nos permite decir que la probabilidad de valores de “t” mayores a 1,73 es mayor que 0,025.
4. El hecho de que la probabilidad asociada al estadístico de prueba sea mayor que la mitad del nivel de significación nos conduce a la decisión de aceptar la hipótesis nula
5. Aceptar la hipótesis nula significa aceptar que el peso promedio al nacimiento es igual en madres adolescentes y madres mayores de 25 años. Ambas muestras provienen de un mismo universo
6. Gráfico del problema
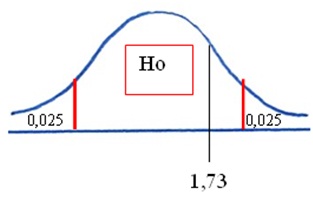
Se observa en el gráfico que la probabilidad del estadístico de prueba es superior a la mitad del nivel de significación (0,025), lo que indica que la diferencia entre las muestras no es significativa.
Comparación de dos muestras con observaciones pareadas
Con el objeto de evaluar el efecto de la instrucción en el conocimiento de los alumnos, se tomó una muestra de 10 alumnos y se compararon las notas obtenidas antes y después de la instrucción.
Los resultados fueron los siguientes.
| Antes: | 4,4 | 3,7 | 4,7 | 2,8 | 4,2 | 4,3 | 3,5 | 3,7 | 3,1 | 1,9 |
| Después: | 4,0 | 5,2 | 5,7 | 4,2 | 4,8 | 3,9 | 4,1 | 3,0 | 4,6 | 6,8 |
Como aquí lo que interesa es evaluar el cambio individual se hace necesario generar una variable que exprese ese cambio. Proponemos entonces crear la variable “x” que exprese la diferencia entre las mediciones individuales. De este modo la variable
x = después-antes
Será nuestra variable de estudio y respecto de ella formularemos la hipótesis nula (esta variable x corresponde a la variable D que anotamos en la fórmula general de la página 23).
![]() plantea que el promedio real (del universo) de las diferencias individuales es cero,
plantea que el promedio real (del universo) de las diferencias individuales es cero,
y la hipótesis alternativa:
![]() plantea que el promedio real de las diferencias es distinto de cero.
plantea que el promedio real de las diferencias es distinto de cero.
Para decidir entre las hipótesis será necesario calcular un estadístico de prueba sobre la base de los valores de la variable “x”:
| Antes | Después | x |
| 4,4 | 4 | -0,4 |
| 3,7 | 5,2 | 1,5 |
| 4,7 | 5,7 | 1 |
| 2,8 | 4,2 | 1,4 |
| 4,2 | 4,8 | 0,6 |
| 4,3 | 3,9 | -0,4 |
| 3,5 | 4,1 | 0,6 |
| 3,7 | 3 | -0,7 |
| 3,1 | 4,6 | 1,5 |
| 1,9 | 6,8 | 4,9 |
El esquema de esta prueba de hipótesis corresponde al utilizado para “comparar un promedio muestral con el promedio del universo”, visto en el capítulo anterior.
Empezaremos calculando promedio y desviación estándar para la variable diferencia (x) y a continuación someteremos a prueba la hipótesis de que el promedio de las diferencias observadas (μ) es igual a cero.
Promedio de la muestra ![]()
Desviación estándar ![]()
Estadístico de prueba será:
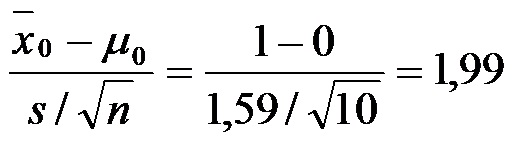
Buscamos ahora en la tabla "t", con 9 (n-1) grados de libertad, la probabilidad asociada a este valor. Mirando la tabla, en la fila de los 9 grados, se observa que el valor asociado a la mitad de alfa (0,025) es 2,262. Como el valor 1,99 se encuentra hacia la izquierda de 2,262 nos conduce a la aceptación de la hipótesis nula.
Por lo tanto el promedio de las diferencias "antes-después" no es significativo, lo que nos permite concluir que, asociado a la intervención educativa, no se observa un aumento significativo del puntaje en los alumnos estudiados.
Comparación de los porcentajes de dos muestras
El problema para el investigador es el siguiente.
En un consultorio urbano, el 28,2% de una muestra de 47 personas presenta algún problema de salud mental. En una muestra de 63 personas de un consultorio rural, el 31% de las personas tiene algún problema de salud mental.
A la luz de estos antecedentes, ¿se puede aceptar la hipótesis de que el porcentaje de problemas de salud mental en el consultorio rural es distinto al del consultorio urbano?
¿Cuáles son los datos que entrega el problema?
| p1= 28,2 | Porcentaje de problemas de salud mental en la muestra urbana. |
| p2= 31 | Porcentaje de problemas de salud mental en la muestra rural. |
| n1= 47 | Tamaño de la muestra urbana. |
| n2= 63 | Tamaño de la muestra rural. |
1. Las hipótesis serán:
![]() y
y ![]()
2. Elegiremos un nivel de significación
![]()
3. El estadístico de prueba será:
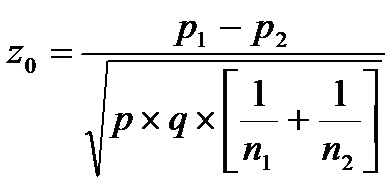
Calcularemos primero el porcentaje común (p)
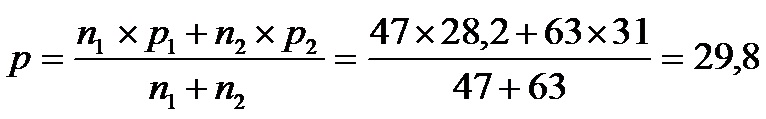
Entonces p=29,8 y q=100-p=70,2.
Luego reemplazamos todos los valores en la fórmula de Z
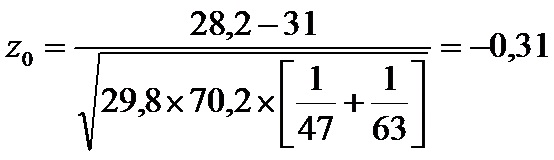
4. Buscamos en la tabla normal la probabilidad asociada a un valor de z menor de -0,31
Resulta 0,3783.
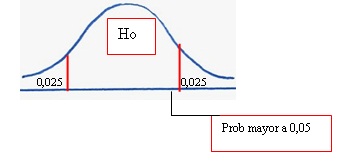
5. Comparamos la probabilidad encontrada con la mitad del nivel de significación
![]()
6. Dado que el valor de z calculado (-0,31) se encuentra más o menos al centro de la curva, su probabilidad, según tabla es de 0,3783 que resulta mayor a la mitad del nivel de significación elegido
Esto nos conduce a la decisión de aceptar la hipótesis nula (ver gráfico).
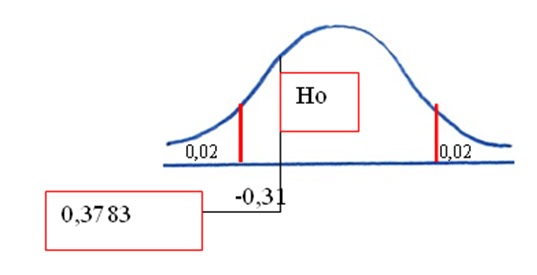
7. Aceptar la hipótesis nula significa aceptar que el porcentaje de problemas de salud mental es similar en ambos consultorios

