Conceptos prácticos en MBE y epidemiología clínica
← vista completaPublicado el 11 de noviembre de 2013 | http://doi.org/10.5867/medwave.2013.10.5826
Estadística para aterrorizados: recomendaciones para describir sus datos
Statistics for the faint of heart – how to display your data
Introducción
La estadística es una parte esencial de cualquier proyecto de investigación biomédica. Tradicionalmente se divide en dos ramas, la estadística descriptiva y la inferencial1. El objetivo de la primera es simplemente mostrar y resumir los datos, mientras que la segunda busca establecer afirmaciones probabilísticas que permitan dar sentido a los hallazgos detectados[1],[2],[3],[4],[5]. En este artículo discutiremos someramente aspectos esenciales respecto a cómo describir datos, sin pretender profundizar a nivel de textos de estadística clásicos.
Describiendo variables cualitativas
Se entiende por variables cualitativas a todas aquellas cuya variabilidad no pueda ser expresada por un número. Dentro de este grupo existen dos subtipos, las variables nominales que sólo pretenden distinguir valores (o categorías) distintos de otro; y las ordinales en las que fuera de distinguirse categorías existe un orden jerárquico dentro de la variable[4],[5]. Ejemplos de la primera son características como el color de ojos, nombres o género, mientras que en la segunda caen formas de expresar gravedad (leve, moderado y severo) o frecuencia (nunca, ocasionalmente, siempre).
Las variables cualitativas pueden describirse de varias maneras. La primera corresponde al simple conteo de eventos dentro de la muestra, vale decir, la frecuencia absoluta de presentación de la categoría. Las frecuencias relativas, como los porcentajes, expresan cuántas veces se expresó un valor determinado en relación al total. En general, se recomienda que los autores utilicen frecuencias absolutas en vez de relativas si sus tamaños muestrales son menores de 100 para evitar confusiones con el uso de porcentajes[6]. Existen además las llamadas frecuencias acumuladas. La frecuencia absoluta acumulada es el número de veces que aparece en la muestra un número igual o inferior a la variable estudiada, mientras que la relativa acumulada representa al cociente entre la anterior cifra con el total de la muestra.
Alternativamente, pueden emplearse una serie de gráficos para expresar los distintos valores que pueden tomar las variables estudiadas. Los más importantes son:
Gráfico circular: en este gráfico las observaciones se dividen en un número de segmentos en un gráfico según las posibles categorías dentro de la variable. Su proporción en relación al gráfico total corresponde a su frecuencia relativa. Si bien son muy utilizados, no se recomienda su uso para expresar variables con más de dos categorías dada la dificultad cognitiva que supone la interpretación visual de áreas[8],[9].
Gráfico de barras: los gráficos de barras expresan las frecuencias observadas en el eje de las abscisas (y). Permiten comparar directamente las alturas observadas por cada categoría en una variable dando una imagen rápida de las formas más frecuentes de presentación. A diferencia de un histograma (véase más adelante), las categorías no son expresadas en intervalos, sino que cada una representa un valor dentro de la muestra[3],[5] y debieran estar separadas por un pequeño espacio una de otra.
Describiendo variables cuantitativas
A diferencia de las anteriores, las variables cuantitativas sí pueden ser expresadas en base a números[1],[2]. Existen dos subtipos: las continuas, en las que entre dos valores cualquiera de la variable existe un número infinito de valores, y las discretas en las que este número es finito. En general, las variables que se miden (estatura, peso, tiempo operatorio) son continuas, mientras que las que se cuentan (número de hijos) son discretas.
La descripción numérica de estas variables se realiza fundamentalmente mediante dos herramientas estadísticas: las medidas de tendencia central y las de dispersión. Las medidas de tendencia central buscan mostrar al centro de los datos, un valor que caracterizará a la mayoría de la muestra. Las más utilizadas son el promedio (o media, suma de todos los valores dividido por el total), la mediana (el valor céntrico de los datos ordenados de menor a mayor) y la moda (valor más repetido). Las medidas de dispersión dan una medida de la heterogeneidad de los datos; grandes medidas de dispersión denotan mayor variabilidad en los datos cuantitativos. Medidas de dispersión de uso común incluyen al rango (valor mínimo y máximo), el rango intercuartil (valores correspondientes al percentil 25 y 75) y la desviación estándar (promedio de las distancias observadas en los valores al contrastarlos con la media)[2],[7],[10],[11].
Todo dato cuantitativo debiera ser descrito con una medida de tendencia central y una de dispersión[1]. La elección de cuál utilizar depende parcialmente de las características de distribución de los datos. Si la variable se distribuye en forma símil a la normal, es recomendable utilizar medias y desviaciones estándar para describirlas. En caso contrario, las medianas y rangos intercuartiles pueden representar una mejor opción[1].
Al igual que con las variables cualitativas, métodos gráficos[5] pueden emplearse en la descripción de variables cuantitativas:
Gráfico de cajas y bigotes: estos gráficos pueden dividirse en dos secciones. La caja corresponde a la sección central y representa a la mayoría de los datos. Al centro está expresada la mediana (o p50) con una línea horizontal. El límite superior de la caja es el p75 y el inferior el p25, lo que corresponde al rango intercuartil. Los bigotes en cambio muestran la variabilidad fuera de la caja, pero dentro de un límite que corresponde a 1,5 veces el recorrido intercuartil (diferencia entre el p75 y p25). Si existen valores más allá de esta frontera, éstos se dibujan como puntos externos al bigote y reciben el nombre de valores extremos o outliers (Figura 1).
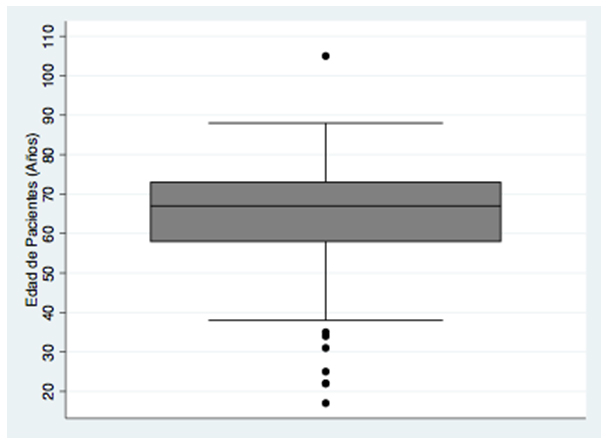 Tamaño completo
Tamaño completo La Figura 1 muestra la mediana de edad de la muestra estudiada que fue de 67 años. El p25 fue 58 años y el p75 fue 73 años. Por tanto, el rango intercuartil es 58 a 73 y el recorrido intercuartil, 15 años (78-53=15). Los bigotes muestran el resto de la variabilidad de la muestra, con un máximo de 1,5 veces el valor del recorrido intercuartil aplicado a los límites de la caja. Por tanto, el límite superior del bigote será 95 años {73+(1,5x15)} y el inferior 36 años {58-(1,5x15)}. Existieron valores que estuvieron más allá de estos límites dentro de la muestra (outliers), denotados con puntos.
Histogramas: los histogramas muestran la distribución de los valores de una variable cuantitativa. En estos gráficos la superficie de cada barra es proporcional a la frecuencia de los valores representados, los que son clasificados en un número de intervalos. De esta manera, estos gráficos pueden detectar asimetrías en los datos observados (o sesgos de una curva) o bien la presencia de otros valores que contienen gran parte de la información de la muestra (distribuciones bimodales), información que puede ser relevante al interpretar los resultados. Si bien son ideales para determinar una distribución de datos, la información descriptiva que aportan es algo menor en relación a los gráficos de cajas y bigotes, por lo que son menos utilizados para estos fines que los anteriores (Figura 2).
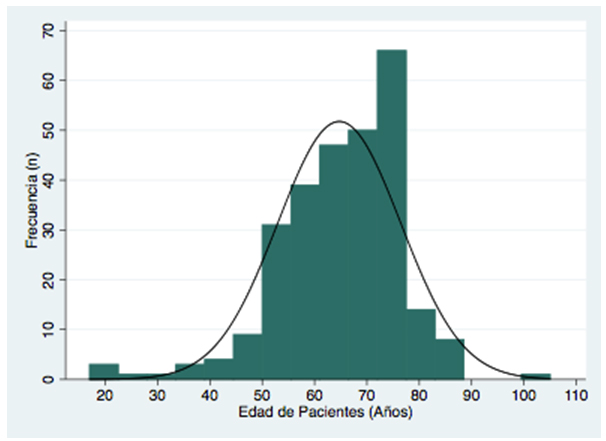 Tamaño completo
Tamaño completo La Figura 2 es el histograma de los mismos datos de la Figura 1, pero en su lugar entrega información respecto a la distribución de los mismos entre los pacientes estudiados. Se aprecia que la distribución sigue una forma de campana y tiene una discreta asimetría favoreciendo a pacientes más jóvenes (sesgo negativo).
Recursos adicionales
Hemos revisado someramente técnicas simples para describir datos en trabajos científicos. Mayor información respecto a estos y otros métodos puede encontrarse en la lista de referencias a continuación.
Notas
Declaración de conflictos de intereses
Los autores han completado el formulario de declaración de conflictos de intereses del ICMJE traducido al castellano por Medwave, y declaran no haber recibido financiamiento para la realización del artículo; no tener relaciones financieras con organizaciones que podrían tener intereses en el artículo publicado, en los últimos tres años; y no tener otras relaciones o actividades que podrían influir sobre el artículo publicado. Los formularios pueden ser solicitados contactando al autor responsable.

