Temas y controversias en bioestadística
← vista completaPublicado el 2 de mayo de 2014 | http://doi.org/10.5867/medwave.2014.04.5944
Manejo de la temporalidad en estudios observacionales para establecer relaciones causales
Temporal sequence in observational studies to establish causality
Resumen
El artículo contiene un breve resumen sobre el alcance de las nociones de causalidad y factor de riesgo y se abordan algunas dificultades operativas para encarar problemas asociados con ellas. Se exalta la vital importancia de la temporalidad y su vínculo con los diseños de investigación observacional más empleados con vistas a discutir relaciones de causalidad. El trabajo expone con detalle la necesidad de registrar el orden en que se producen los acontecimientos relevantes y luego contemplarlo en el análisis. Se ofrece un detallado ejemplo de los errores en que se suele incurrir y el efecto que tales errores pueden producir.
1. Introducción
La determinación de los elementos que gravitan sobre la realidad de manera causal es una tarea que, implícita o explícitamente, se trazan a diario los investigadores en el marco de la clínica, la salud pública y la epidemiología. Ante la dificultad operativa de satisfacer las demandas metodológicas asociadas, muchas veces se erigen en calidad de objetivos ciertos sucedáneos que no apuntan realmente al propósito objetivamente deseado aunque aparentan hacerlo. La más común de estas formulaciones consiste en comunicar qué se quiere establecer si determinado factor “se asocia” a cierto desenlace, como si valorarlo tuviera algún interés intrínseco.
La medición de asociación es un mero intermediario metodológico de tipo estadístico, de modo que transformarlo en un objetivo es una especie de autoengaño que no sólo no sirve para resolver el problema verdadero, sino que ocasionalmente conduce a consolidar convicciones erróneas en torno a él.
La presente contribución procura exponer algunas ideas centrales sobre este asunto; especialmente, se propone precaver contra uno de los errores básicos que se cometen con frecuencia, así como dar algunas sugerencias prácticas e ilustrarlo con un ejemplo elocuente.
2. Definición de causa y algunas consideraciones operativas
La definición de causa en su sentido epidemiológico ha dado lugar a una controversia que ya dura décadas [1],[2],[3],[4]. Más allá de otras consideraciones teóricas, una definición potencialmente útil acerca de aquello que podemos entender como “causa” de un “efecto” dado puede expresarse del modo siguiente: cualquier factor, condición o característica, cuya supresión elimina la posibilidad de que se produzca el efecto, es una causa del mismo [5]. Si bien tal definición aparenta ser funcional, no siempre resulta operativamente fecunda.
Una noción diferente, pero de máximo interés en este contexto, es la de factor de riesgo, que ocasionalmente genera confusión, pues estos aparecen acompañados de las causas y "se parecen" a ellas. Se trata de factores asociados al efecto que, sin ser imprescindibles para que éste se produzca, pueden favorecer que el agente causal actúe [6]. Un ejemplo recurrente es el hábito de fumar como elemento propiciatorio de afecciones respiratorias.
En 1965, Bradford Hill pronuncia su trascendente y bien conocido discurso ante la Sección de Medicina Ocupacional de la Royal Society of Medicine [7] donde se discuten varias pautas de causalidad a considerar en estudios epidemiológicos.
El núcleo de su discurso parte de que se ha observado una asociación entre dos fenómenos. Su intensidad puede valorarse a través de indicadores tan diversos como, por ejemplo, un riesgo relativo o un odds ratio (entre dos variables dicotómicas), un coeficiente de correlación lineal (entre dos variables cuantitativas) o una diferencia de medias aritméticas (entre una variable dicotómica y una cualitativa), y su existencia es condición sine qua non de la causalidad.
A modo de recordatorio, repasemos el caso en que se trata de dos variables binarias para las cuales se computa el odds ratio (OR). Este sencillo y extendido recurso es el que se empleará en el ejemplo que se incluye en la Sección 6. La situación se resume en la Tabla I, donde se contempla determinado factor de riesgo y cierta enfermedad.
 Tamaño completo
Tamaño completo Los cálculos convencionales serían:
a) El odds ratio ![]() con el que se estima cuántas veces más peligroso resulta la presencia de determinado factor a los efectos de enfermar (respecto de quien no tiene ese factor)
con el que se estima cuántas veces más peligroso resulta la presencia de determinado factor a los efectos de enfermar (respecto de quien no tiene ese factor)
b) Intervalo de confianza para el OR, que se computa mediante ![]() , donde
, donde ![]()
c) El valor ![]() donde
donde ![]() es una variable que se distribuye Ji-Cuadrado con un grado de libertad y
es una variable que se distribuye Ji-Cuadrado con un grado de libertad y ![]() Si p es menor que 0,05 se declara que el OR dista significativamente de la unidad (es decir, que hay una asociación estadísticamente significativa); en caso contrario, que no se tiene suficiente evidencia muestral para descartar el azar como explicación de la asociación observada.
Si p es menor que 0,05 se declara que el OR dista significativamente de la unidad (es decir, que hay una asociación estadísticamente significativa); en caso contrario, que no se tiene suficiente evidencia muestral para descartar el azar como explicación de la asociación observada.
Trátese de un OR o de otra forma de asociación, cuanto más intensa sea esta, más verosimilitud adquiere la hipótesis subyacente de que el factor favorece la aparición de la enfermedad.
Los criterios de Hill pueden constituir pautas de utilidad en el estudio de una asociación pero, como él mismo advirtiera [8], no han de considerarse mandamientos ineludibles de valor universal, ni mucho menos pueden concebirse como garantía para la causalidad. De todas ellas, nos concentraremos en la más obvia, la menos discutible y que, sin embargo, es fuente de costosos errores y objeto de frecuente desatención: que la presunta causa ha de preceder al efecto.
3. Orígenes para una asociación observada
Cualquier asociación observada entre dos variables X e Y puede tener varios orígenes o explicaciones posibles.
Uno de los más importantes es el efecto de sesgos (de medición, de memoria, de selección, etcétera); los cuales pueden evitarse adoptando determinadas precauciones, o enmendarse mediante acciones oportunas. Esta es un área que ha sido objeto de gran atención especializada [9] y que será atendida en otras contribuciones de la presente serie de artículos.
Otra explicación posible para la observación de una asociación concierne a los llamados factores de confusión, variables que se relacionan tanto con el supuesto factor causal (exposición) como con el desenlace (efecto) siempre que no sean un estadio intermedio en la secuencia causal que va de la exposición al efecto [10]. Tal explicación se puede descartar ocasionalmente en la fase de diseño, por ejemplo a través de la asignación aleatoria de los sujetos a los tratamientos, o imponiendo restricciones tales como el emparejamiento de casos y controles. Pueden asimismo controlarse durante la fase de análisis usando diversas técnicas (posestratificación, regresión logística, correlación parcial, tipificación, análisis de covarianza, entre otros). Si la asociación persiste una vez aplicados tales recursos, se puede seguir pensando que el vínculo sea causal.
Una tercera posibilidad es que la asociación se haya observado meramente por azar. Para descartarla, el recurso convencional es la prueba de significación. Según este enfoque, si la asociación no es suficientemente grande como para ser “estadísticamente significativa”, entonces no se podría descartar el azar como explicación de haberla observado. Lo más recomendado en la actualidad, sin embargo, no es pronunciarse binariamente sobre si la existe o no cierta asociación, sino aquilatar su magnitud usando intervalos de confianza [11].
Si el examen de estos tres posibles orígenes para la asociación (sesgos, influencia externa, azar) no aporta elementos sustantivos que expliquen que la hayamos observado, entonces solamente quedan dos posibilidades: X es causa de Y, o Y es causa de X. Solo el análisis temporal si se dan las condiciones para realizarlo permite pronunciarse a favor de uno u otro. De lo que se trata es de garantizar que tales condiciones se den.
4. Los diseños según manejo de la temporalidad
En el campo de la investigación biomédica se emplean diversos ejes para clasificar los estudios. Aquí, sin embargo, nos detendremos en el eje temporal, que abarca tres posibilidades básicas:
a) Estudios transversales (típicamente, de índole descriptiva)
b) Estudios retrospectivos (virtualmente circunscritos a la metodología de casos y controles)
c) Estudios prospectivos (que pudieran ser “de cohorte”, también conocidos como follow up o seguimientos o estudios experimentales que, por su naturaleza, tienen necesariamente ese carácter)
Cualquiera de ellos es, en principio, potencialmente útil en el proceso de identificar tanto las causas de ciertos desenlaces como los factores de riesgo que se asocian a ellos, pero en todos los casos ha de contemplarse la llamada premisa de precedencia temporal, objeto de la siguiente sección.
5. Premisa de precedencia temporal
Ningún análisis de causalidad tiene un sentido claro cuando el diseño del estudio no ha tenido en cuenta una demanda tan básica como lo que podemos llamar “premisa de precedencia temporal” (PPT) [12]. Ella establece que en los estudios que procuran evaluar relaciones de causalidad debe registrarse el orden en que se producen los acontecimientos, atendiendo al hecho de que la presunta causa de cierto efecto ha de precederle en el tiempo. Esta es una condición metodológicamente imprescindible, trátese de un factor de riesgo o de una causa.
Los estudios prospectivos, en los cuales, como su nombre indica, los hechos se miden en orden temporalmente ascendente, no suelen presentar dudas acerca del cumplimiento de la PPT, ya que en estos la observación comienza cuando aún no se han producido los desenlaces que se estudian.
En los transversales y retrospectivos, donde se debe indagar sobre hechos ocurridos con anterioridad al momento del estudio, la dificultad radica en que es imposible establecer mediante observación cuál fue el orden en que ocurrieron los hechos que se registran (solo puede intentarse la reconstrucción de los acontecimientos). Son por ello altamente vulnerables al no cumplimiento de la PPT. En tales estudios, además de sujetos sanos, se incluyen individuos que en el momento de la encuesta padecen de una enfermedad. Si se quiere evaluar el posible efecto causal de cierta condición, rasgo, conducta o, más generalmente, de una “exposición”, en el desarrollo de la enfermedad, lo que realmente interesa registrar no es si el sujeto está sometido a tal exposición en el momento del estudio, sino si lo estaba o no antes de que enfermara.
Cuando no se tiene en cuenta este "detalle", se cancela toda interpretación potencial de sus resultados a los efectos del estudio de causalidad. Este hecho puede ser catastrófico, aunque muchos investigadores no lo tomen en cuenta, o lo consideren como un mal menor. El ejemplo que se desarrolla a continuación ilustra claramente el problema.
6. Una ilustración elocuente
Imaginemos que en cierta ciudad hay tres equipos independientes de investigadores, todos los cuales han encarado la misma tarea investigativa: quieren evaluar el grado en que el consumo de golosinas contribuye al desarrollo de obesidad entre escolares. Cabe enfatizar que no se trata de valorar si el consumo está “asociado” a la dolencia, sino si puede o no considerar un factor de riesgo o una causa para su aparición. Lo primero es un mero acto estadístico; lo segundo es lo que realmente se discute.
Cada uno de dichos equipos empleó su propia estrategia investigativa en el intento de responder esta pregunta.
6.1 Estudio de cohorte
El primer equipo (Equipo A) inició el estudio en 2008 tomando una muestra de 1150 niños que en ese momento tenían dos años cumplidos pero menores de tres años. De ellos, 100 eran obesos, de modo que los suprimieron de la muestra y se quedaron con 1100 infantes, todos libres de obesidad. En ese momento identificaron los hábitos de consumo de golosinas de cada uno de ellos y conformaron dos grupos: 700 niños que comían golosinas regularmente* y 400 que no lo hacían. Planificaron la estimación de la incidencia de obesidad en cada uno de dichos grupos. La Figura 1 muestra la estructura de este análisis.
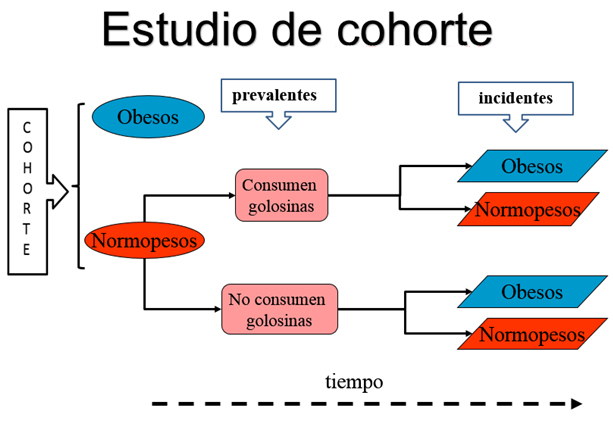 Tamaño completo
Tamaño completo Algunos niños comenzaron a engordar en ambos grupos y tres años después, en 2011 (cuando todos tienen cinco años cumplidos), se valora el sobrepeso de cada miembro de la cohorte. El estudio arroja lo siguiente: entre los 700 consumidores, 400 desarrollaron obesidad (el 57%), mientras que entre los 400 no consumidores, se registraron en ese momento 120 niños obesos (30%). La Tabla II resume la situación.
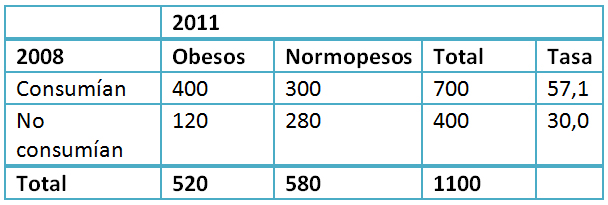 Tamaño completo
Tamaño completo La tasa de incidencia acumulada de obesidad es casi el doble entre quienes tenían el hábito que entre los que no lo tenían. El OR es 3,1; ![]() y la p asociada es virtualmente nula (la asociación es estadísticamente muy significativa); el intervalo de confianza es igual a (2,4-4,0), lo cual indica que podemos estar altamente confiados de que el consumo de golosinas, como mínimo, incrementa en un 240% el riesgo de enfermar. Este estudio longitudinal o de cohorte, entonces, ofrece indicios empíricos muy fuertes de que el consumo de golosinas contribuye sustantivamente a la aparición de la obesidad.
y la p asociada es virtualmente nula (la asociación es estadísticamente muy significativa); el intervalo de confianza es igual a (2,4-4,0), lo cual indica que podemos estar altamente confiados de que el consumo de golosinas, como mínimo, incrementa en un 240% el riesgo de enfermar. Este estudio longitudinal o de cohorte, entonces, ofrece indicios empíricos muy fuertes de que el consumo de golosinas contribuye sustantivamente a la aparición de la obesidad.
6.2 Efecto de una campaña preventiva
Supongamos que en ese momento (2011) empieza una campaña para desestimular el consumo de golosinas en la ciudad, con énfasis en el daño que producen a los efectos de desarrollar y consolidar obesidad.
Transcurridos dos años, en 2013, dicha campaña arroja resultados tangibles. En materia de consumo, el 45% de los obesos que consumían golosinas en la ciudad, dejan de hacerlo, en tanto que también se consigue una disminución de dicho consumo entre los que no son obesos: el 5% de los 300 normopesos que consumían golosinas, también dejan de hacerlo. En este último caso, naturalmente, el efecto de la intervención es más reducido, algo razonable, pues la campaña, aunque influye en toda la comunidad, incide con mucha más fuerza entre los que tienen la dolencia (obesidad) que en el resto. En general, por otra parte, la prevalencia global de obesos se redujo en un 8%.
6.3 Estudio transversal
El Equipo B realiza su estudio en 2013 para estimar la asociación que exhiben las dos variables relevantes en ese momento. Este equipo actúa de manera independiente a la del Equipo A, salvo por el hecho de que decide aprovechar la muestra empleada por este; para cada uno de sus miembros se indaga si es obeso o no, así como si consume o no regularmente golosinas. Nótese que esta era una muestra representativa de niños cuando tenían dos años; ahora lo es, esencialmente, de los niños que tienen siete años**.
La Figura 2 muestra el procedimiento seguido por el Equipo B.
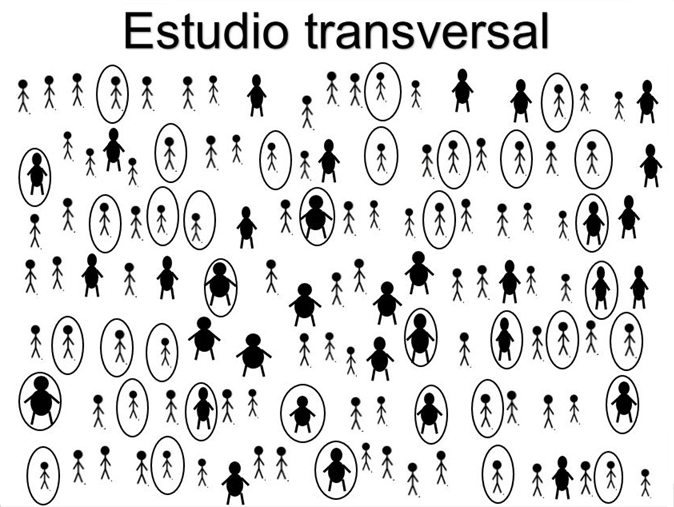 Tamaño completo
Tamaño completo Las consecuencias de la intervención descrita en la sección precedente, naturalmente, se reflejan en la muestra: el número de obesos pasa a ser 478 (92% de 520), en tanto que el número de consumidores de golosinas entre los obesos, pasa de 400 a 240; entre los normopesos, hay 15 consumidores menos (el número pasa de 300 a 285). Siendo así, la Tabla II adopta el contenido que recoge la Tabla III.
 Tamaño completo
Tamaño completo Los porcentajes de obesos entre consumidores y no consumidores actuales de golosinas son bastante similares (ligeramente superior entre los primeros que entre los segundos). El OR es 1,2 y ![]() A esta pequeña asociación le corresponde una p=0,15, que desautoriza a declararla estadísticamente significativa. El intervalo de confianza es igual a 0,9-1,5. En este escenario, en síntesis, no se ha alcanzado evidencia muestral que permita aseverar que hay asociación real entre consumo de golosinas y obesidad.
A esta pequeña asociación le corresponde una p=0,15, que desautoriza a declararla estadísticamente significativa. El intervalo de confianza es igual a 0,9-1,5. En este escenario, en síntesis, no se ha alcanzado evidencia muestral que permita aseverar que hay asociación real entre consumo de golosinas y obesidad.
¿Cómo se explica que el estudio del equipo B haya arrojado que no hay “asociación” a pesar de que sabemos, gracias al estudio del Equipo B, que una variable influye sobre la otra? Sencillamente porque el Equipo B no estimó tasas de incidencia sino concomitancia factual. Puesto que en este escenario no se tuvo en cuenta la temporalidad, en una mirada transversal, efectivamente, no la hay. Esto se debe a que estamos ante la típica situación en que X influye en Y, pero también Y influye en X (los patrones de consumo pueden influir en la obesidad y, a la vez, la obesidad influye en los patrones de consumo, especialmente si, además, hubo una intervención).
Para entenderlo mejor, observemos que si los cambios en los patrones de consumo no dependieran de la condición morbosa, entonces no se habría producido lo que acabamos de exponer. Por ejemplo, si además de producirse una reducción global de la tasa de obesos de un 8%, las tasas de consumidores entre obesos y no obesos se hubieran reducido por igual, digamos, si el 20% de los niños, tanto de uno como de otro tipo, hubieran dejado de consumir golosinas gracias a la campaña, entonces la realidad transversalmente mirada hubiera sido como se ve en la Tabla IV.
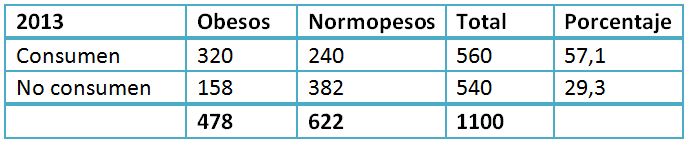 Tamaño completo
Tamaño completo Los números cambian, pero se obtiene un OR de 3,2 (casi igual que el que arrojó el estudio de cohorte), un valor de p sumamente pequeño y tasas de obesidad muy parecidas a las de aquel estudio de cohorte (Tabla II). El intervalo de confianza también sería muy similar: 2,5-4,1.
Los resultados del equipo B se explican, en suma, porque la tabla correspondiente se configuró luego de preguntar lo que no interesaba a los efectos de evaluar la gravitación del consumo: se preguntó qué está pasando con dicho consumo en 2013 en lugar de qué estaba ocurriendo durante el lapso previo al momento en que se registra la obesidad (es decir, qué estaba pasando con el consumo de golosinas al comienzo del período 2011-2013).
6.4 Un estudio de casos y controles
Para cerrar la ilustración, supongamos finalmente que el Equipo C realizó un estudio de casos y controles (obesos y normopesos respectivamente). Imaginemos que, de la muestra, en 2013 se toman 150 sujetos con la primera de esas condiciones y 300 con la otra (dos controles por cada caso), y que se indaga para cada uno de esos 450 niños acerca de la práctica que tenía en materia de consumo durante el período 2008 – 2011.
Este enfoque puede expresarse gráficamente como se muestra en la Figura 3.
 Tamaño completo
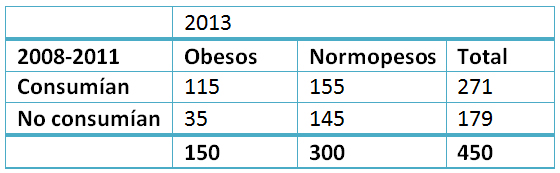
Tamaño completo El número de individuos que consumían entonces golosinas entre obesos (teniendo en cuenta las tasas de la Tabla II y suponiendo que esos datos pudieran realmente obtenerse de manera fidedigna), sería igual a 115 (el 77% de 150, ya que 400 es el 76,9% de 520) y la misma operación para normopesos arrojaría un total de 155 sujetos (52% de 300, porque 300 es el 51,7% de 580). Los resultados serían los que se recogen en la Tabla V.
 Tamaño completo
Tamaño completo El Equipo C no puede computar tasas de incidencia de obesidad entre consumidores ni entre no consumidores. Por ejemplo, sería erróneo decir que el 43% (115 de 271) de los consumidores desarrollan obesidad, y también lo sería afirmar que eso ocurre en el 20% (35 de 179) de los no consumidores, debido a que la muestra de 450 niños con que opera todo estudio de casos y controles no es representativa de la población.
Pero sí se puede estimar la razón de odds de consumo entre obesos y entre normopesos (OR), que asciende a 3,1 el mismo que se obtuvo en el estudio longitudinal que resulta ser, como antes, estadísticamente muy significativo. El intervalo de confianza para este parámetro resulta ser 2,0-4,8. Nótese que este intervalo, aunque esencialmente similar en cuanto a la interpretación, es más ancho (menos informativo) que el que había obtenido el Equipo A. Ello se debe a que el estudio de casos y controles operó con una muestra mucho menor que la que se empleó en la de cohortes.
Sintetizando, la medición que dio lugar a la Tabla II es peor que estéril sea, en realidad, contraproducente a los efectos de evaluar el papel causal del consumo de golosinas. El Equipo B preguntó lo que no interesaba y paga las consecuencias al obtener un OR que no se puede recuperar conceptualmente en modo alguno. El Equipo C realizó su estudio en el mismo momento que el B (año 2013) pero consiguió reconstruir lo que ocurría en el pasado e incorporar esa información en el análisis. Siendo así, obtuvo prácticamente lo mismo que había hallado el Equipo A. Los resultados del Equipo C no son tan precisos como los del A, y están sujetos a sesgos (por ejemplo de memoria de las madres, que aquí se han considerado inexistentes) que no aquejaban al A, pero no conducen a una conclusión errónea como la que obtuvo el Equipo B.
* Qué habrá de entenderse por “consumo regular” de golosinas es ahora irrelevante. Se supone que se ha establecido una definición operativa inequívoca.
** En rigor, la muestra no es de la población de todos los niños, sino de aquellos que no eran obesos a los dos años. Pero el porcentaje de obesos en aquel momento era mínimo (4%), de modo que esta exclusión no modifica apreciablemente los cálculos que siguen.

